Skip to main content
欢迎来到PAWPAW技术文档网站，了解更多信息。

Fast Fourier Transform API

本文档包含lib_xcore_math库中的快速傅里叶变换（FFT）API，这些API提供了多种操作的能力。包含单个实信号、复数信号以及一对实信号的BFP FFT。同时，也覆盖了包括频谱打包、时域分解以及频域分解等专项操作的相关API。

FFT API快速参考​

简述正向函数逆向函数
单个实信号的BFP FFTbfp_fft_forward_mono()bfp_fft_inverse_mono()
单个复数信号的BFP FFTbfp_fft_forward_complex()bfp_fft_inverse_complex()
一对实信号的BFP FFTbfp_fft_forward_stereo()bfp_fft_inverse_stereo()
BFP频谱打包bfp_fft_unpack_mono()bfp_fft_pack_mono()
低级别的时域分解FFTfft_dit_forward()fft_dit_inverse()
低级别的频域分解FFTfft_dif_forward()fft_dif_inverse()
float类型实信号的FFTfft_f32_forward()fft_f32_inverse()

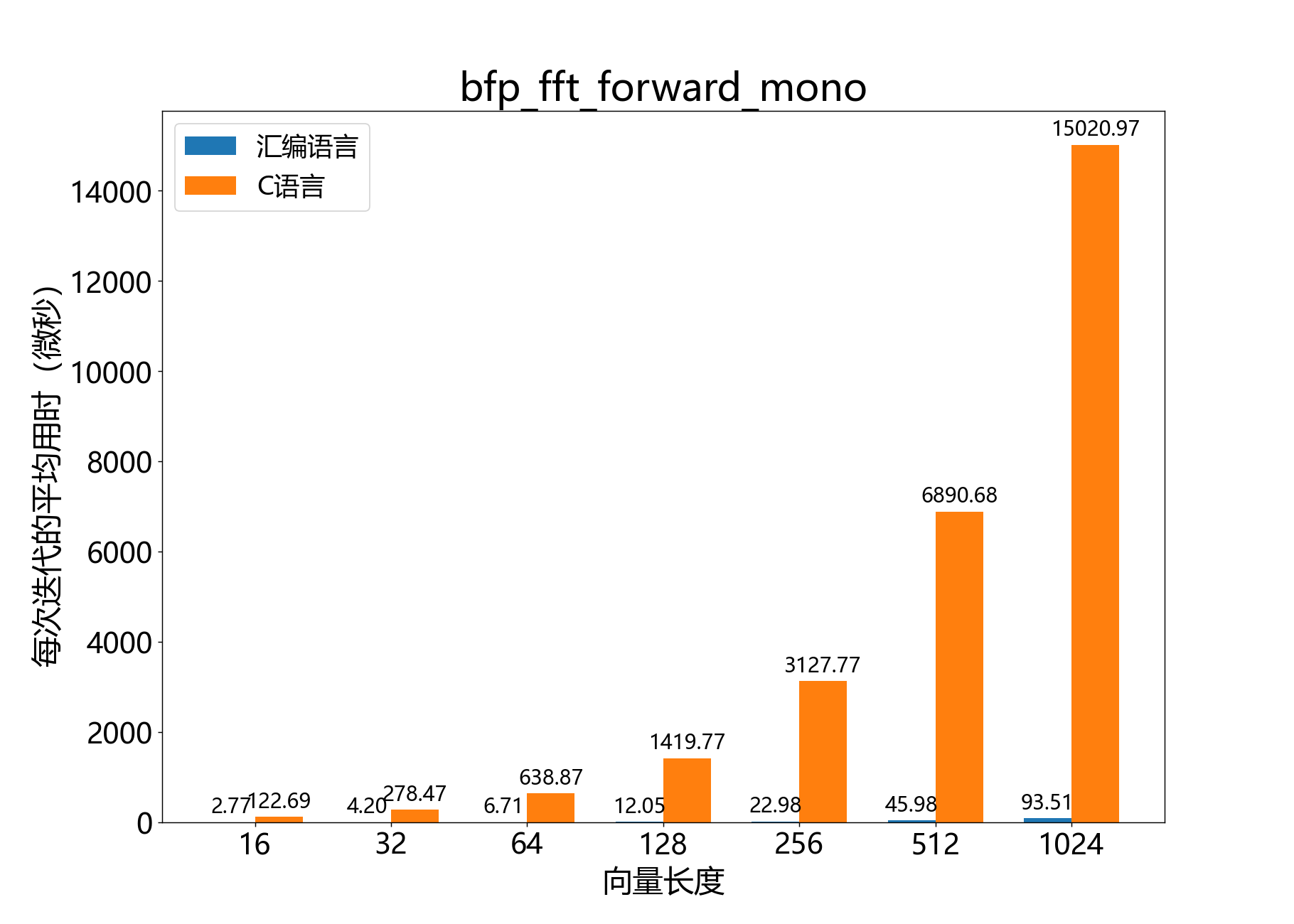
bfp_complex_s32_t* bfp_fft_forward_mono()​

在实数32位序列上执行正向离散傅里叶变换（DFT）。

该函数对实数32位BFP向量x执行NN点正向实数DFT，其中NN为x->length。

// 示例
// 使用样本初始化时域数据。
int32_t buffer[N] = { ... };
bfp_s32_t samples;
bfp_s32_init(&samples, buffer, 0, N, 1);
// 执行正向DFT
{
    bfp_complex_s32_t* spectrum = bfp_fft_forward_mono(&samples);
    ...
}

参数：

  • bfp_s32_t* x – [inout] 要进行DFT的BFP向量x[n]x[n]。

返回值：

  • x的地址，强制转换为bfp_complex_s32_t*。

参考性能:

bfp_fft_forward_mono

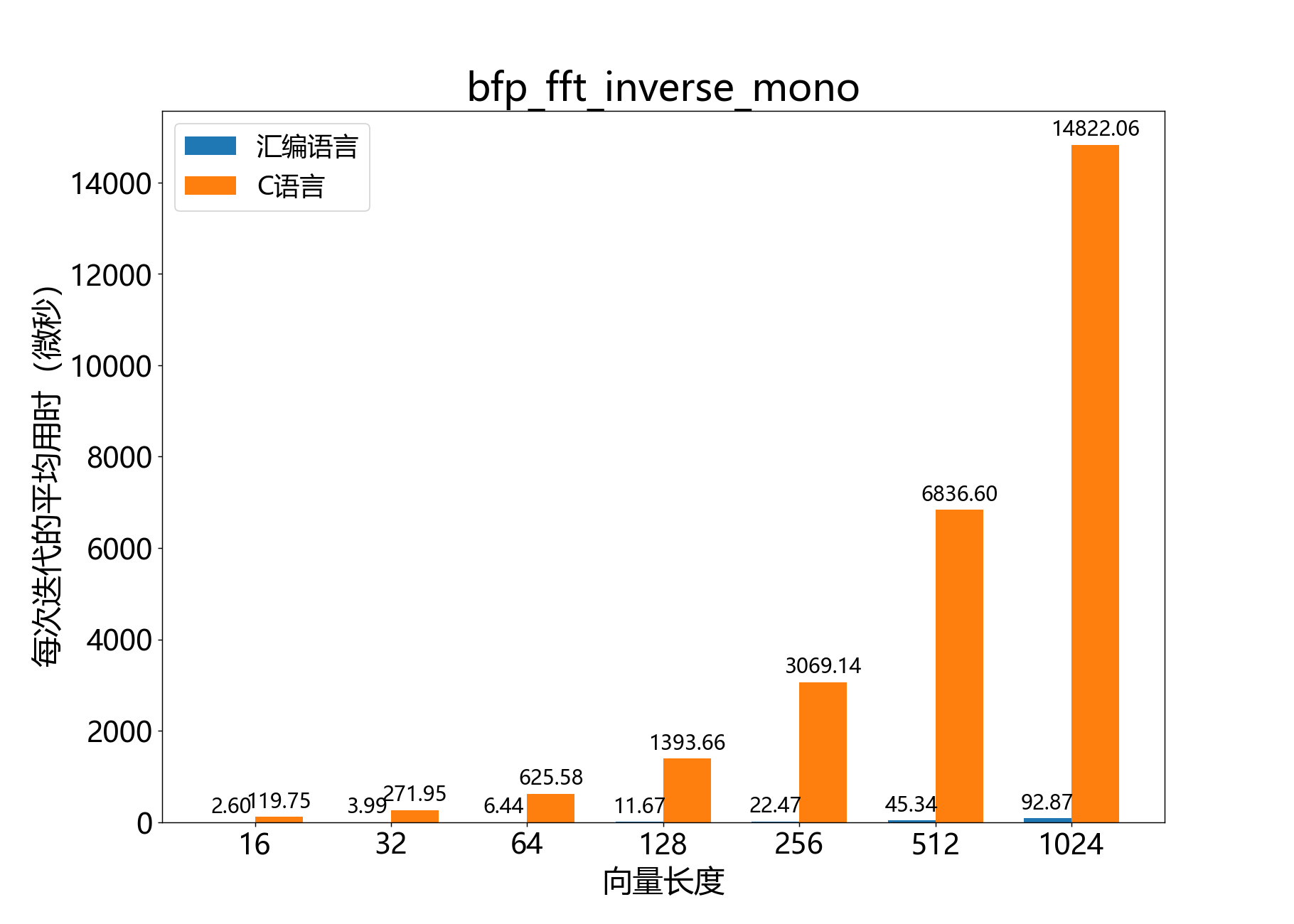
bfp_s32_t* bfp_fft_inverse_mono()​

在复数32位序列上执行逆向实数离散傅里叶变换（IDFT）。

该函数对复数32位BFP向量x执行NN点逆向实数DFT，其中NN为2*x->length。

// 示例
// 使用样本初始化时域数据。
int32_t buffer[N] = { ... };
bfp_s32_t samples;
bfp_s32_init(&samples, buffer, 0, N, 1);
// 执行正向DFT
{
    bfp_complex_s32_t* spectrum = bfp_fft_forward_mono(&samples);
    ...
    bfp_fft_inverse_mono(spectrum);
}

参数：

  • bfp_complex_s32_t* x – [inout] 要进行IDFT的BFP向量X[f]X[f]。

返回值：

  • x的地址，强制转换为bfp_s32_t*。

参考性能:

bfp_fft_inverse_mono

void bfp_fft_forward_complex()​

在复数32位序列上执行正向复数离散傅里叶变换（DFT）。

该函数对复数32位BFP向量x执行NN点正向复数DFT，其中NN为x->length。

// 示例
// 使用样本初始化复数时域数据。
complex_s32_t buffer[N] = { ... };
bfp_complex_s32_t vector;
bfp_complex_s32_init(&vector, buffer, 0, N, 1);
// 执行正向DFT
bfp_fft_forward_complex(&vector);
...

参数：

  • bfp_complex_s32_t* x – [inout] 要进行DFT的BFP向量x[n]x[n]。

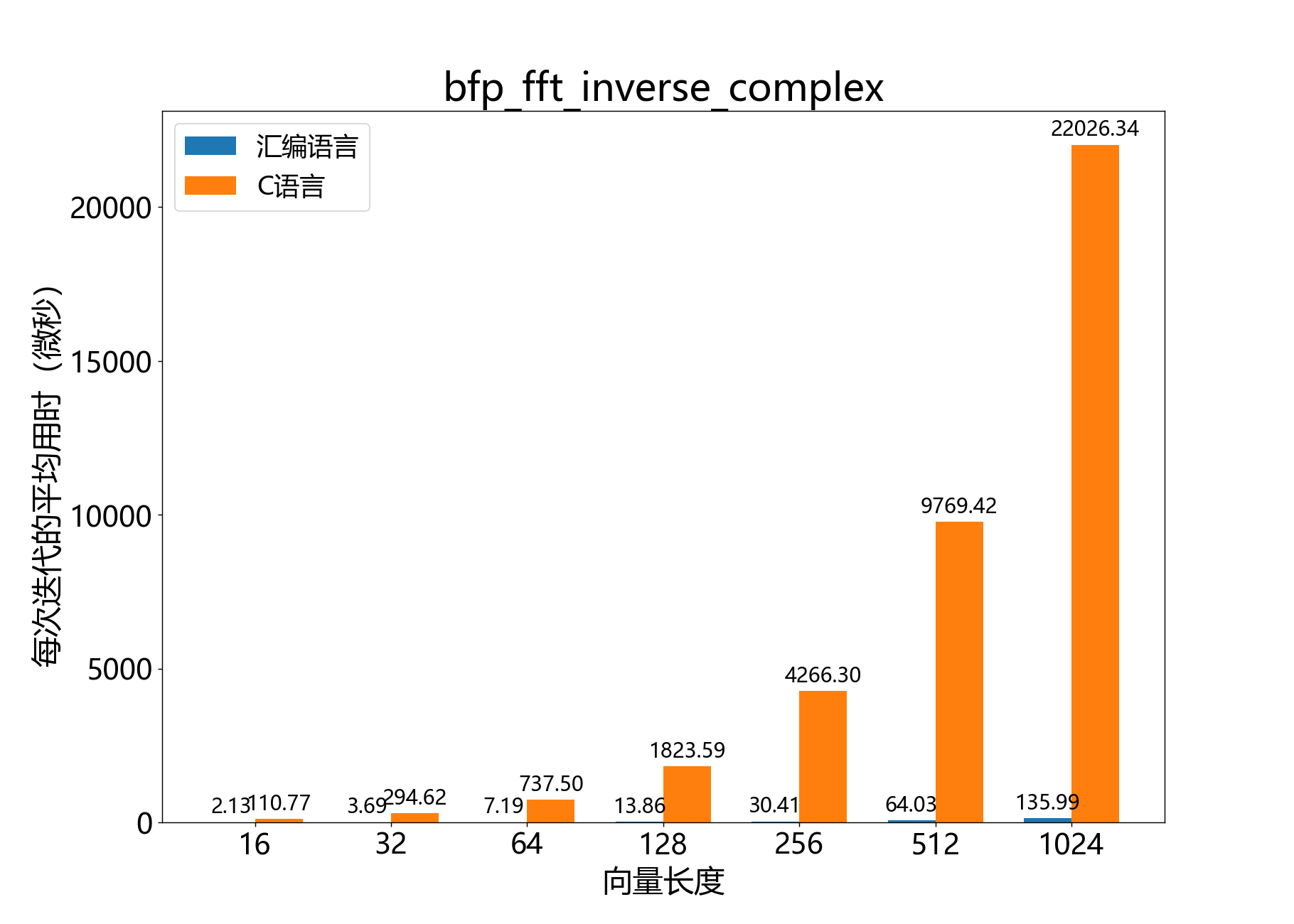
void bfp_fft_inverse_complex()​

在复数32位序列上执行逆向复数离散傅里叶变换（IDFT）。

该函数对复数32位BFP向量x执行NN点逆向复数DFT，其中NN为x->length。

// 示例
// 使用样本初始化复数时域数据。
complex_s32_t buffer[N] = { ... };
bfp_complex_s32_t vector;
bfp_complex_s32_init(&vector, buffer, 0, N, 1);
// 执行正向DFT
bfp_fft_forward_complex(&vector);
...
bfp_fft_inverse_complex(&vector);
...

参数：

  • bfp_complex_s32_t* x – [inout] 要进行IDFT的BFP向量x[n]x[n]。

参考性能:

bfp_fft_inverse_complex

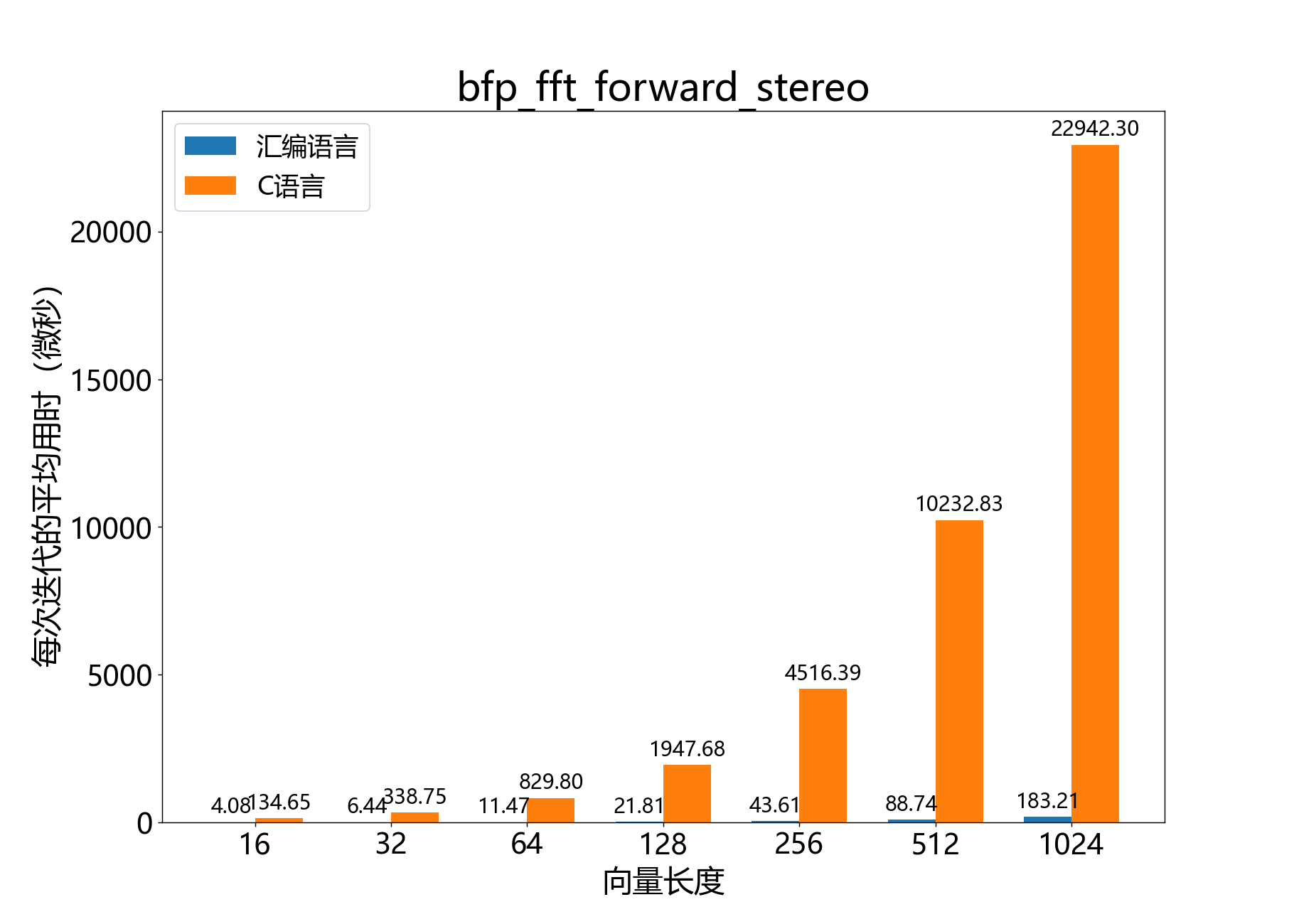
void bfp_fft_forward_stereo()​

注意：目前不建议使用此函数。它可以正常工作，但是库的最近更改（即不再支持通道对向量）意味着此函数在计算效率上不比分别在每个输入向量上调用 bfp_fft_forward_mono() 更高。此外，此函数目前需要一个临时缓冲区，而单声道FFT则不需要。

对一对实数32位序列执行正向离散傅里叶变换（DFT）。

该函数对实数32位BFP向量 aˉ\bar a 和 bˉ\bar b 执行 NN 点正向实数DFT，其中 NN 是 a->length（必须等于 b->length）。结果频谱 Aˉ\bar A 和 Bˉ\bar B 存放在 a 和 b 中。每个频谱是一个 N/2N/2 元素的复数32位BFP向量。在调用此函数后，可以将指针 a 和 b 强制转换为 bfp_complex_s32_t* 来访问频谱。

操作：

A[f]=∑n=0N−1(a[n]⋅e−j2πfn/N)，其中 0≤f≤N/2A[f] = \sum_{n=0}^{N-1} \left( a[n]\cdot e^{-j2\pi fn/N} \right) \text{，其中 } 0 \le f \le N/2

B[f]=∑n=0N−1(b[n]⋅e−j2πfn/N)，其中 0≤f≤N/2B[f] = \sum_{n=0}^{N-1} \left( b[n]\cdot e^{-j2\pi fn/N} \right) \text{，其中 } 0 \le f \le N/2

示例：

// 使用样本初始化时域数据。
int32_t bufferA[N] = { ... };
int32_t bufferB[N] = { ... };
complex_s32_t scratch[N]; // 临时缓冲区 - 内容不重要
bfp_s32_t channel_A, channel_B;
bfp_s32_init(&channel_A, buffer, 0, N, 1);
bfp_s32_init(&channel_B, buffer, 0, N, 1);

// 执行正向DFT
bfp_fft_forward_stereo(&channel_A, &channel_B, scratch);
      
// channel_A 和 channel_B 现在应被视为已修改，因为结构体现在实际上是 bfp_complex_s32_t
bfp_complex_s32_t* chanA = (bfp_complex_s32_t*) &channel_A;
bfp_complex_s32_t* chanB = (bfp_complex_s32_t*) &channel_B;

// 使用 `chanA` 和 `chanB` 对频域数据进行操作
...
// 执行逆DFT以返回时域
bfp_fft_inverse_stereo(&chanA, &chanB, scratch);
      
// 再次使用 channel_A 和 channel_B 来使用新的时域数据
...

参数：

  • bfp_s32_t *a – [inout] [out] 时域BFP向量 aˉ\bar a。[out] 频域BFP向量 Aˉ\bar A
  • bfp_s32_t *b – [inout] [out] 时域BFP向量 bˉ\bar b。[out] 频域BFP向量 Bˉ\bar B
  • complex_s32_t scratch[] – 至少包含 a->length 个 complex_s32_t 元素的临时缓冲区

参考性能:

bfp_fft_forward_stereo

void bfp_fft_inverse_stereo()​

注意

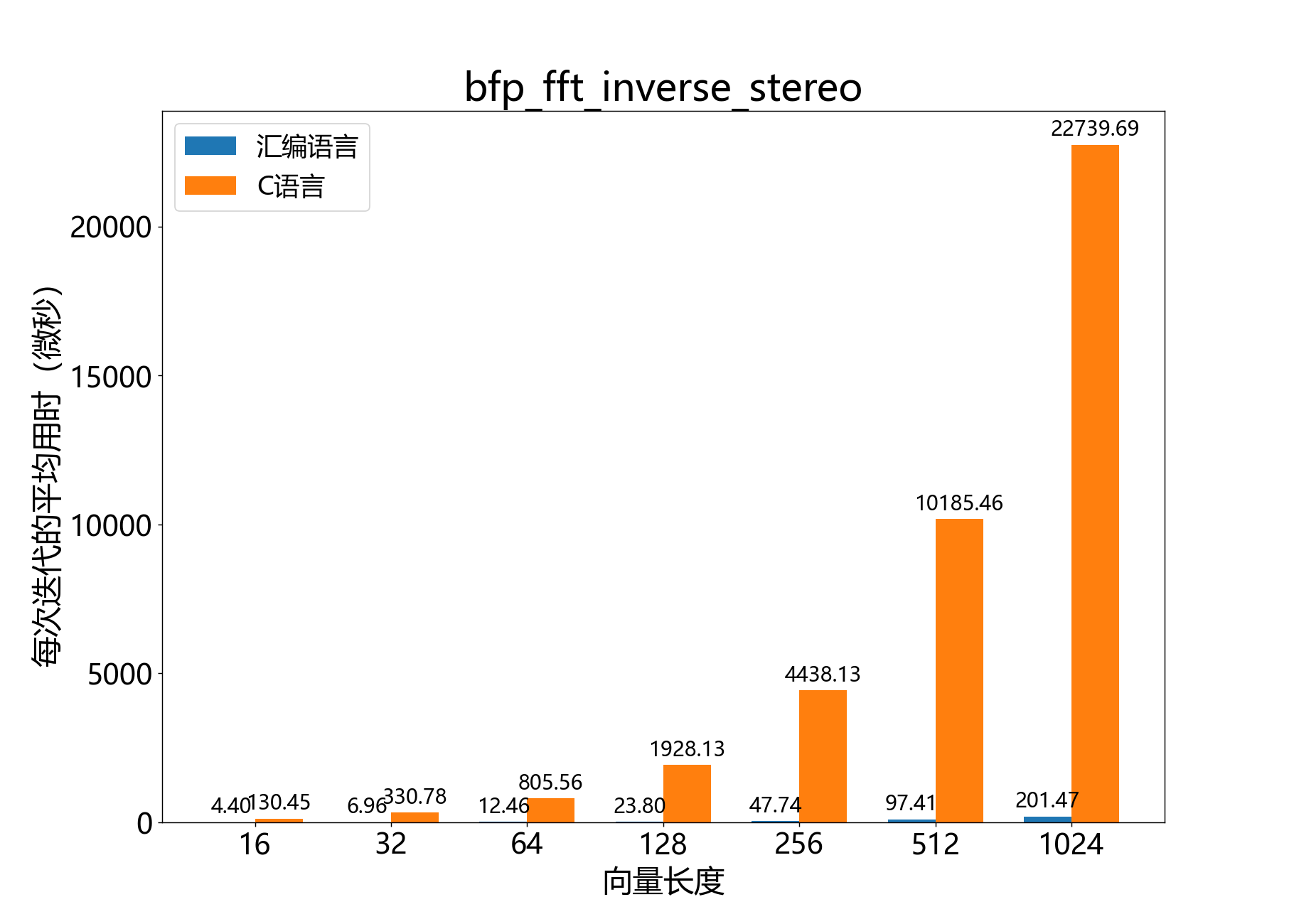
目前不建议使用此函数。它可以正常工作，但是库的最近更改（即不再支持通道对向量）意味着此函数在计算效率上不比分别在每个输入向量上调用 bfp_fft_forward_mono() 更高。此外，此函数目前需要一个临时缓冲区，而单声道FFT则不需要。

对一对复数32位序列执行逆向离散傅里叶变换（IDFT）。

该函数对复数32位BFP向量 Aˉ\bar A 和 Bˉ\bar B（分别为 A_fft 和 B_fft）执行 NN 点逆向实数DFT，其中 NN 是 A_fft->length。结果时域信号 aˉ\bar a 和 bˉ\bar b 存放在 A_fft 和 B_fft 中。每个时域结果是一个 N/2N/2 元素的实数32位BFP向量。在调用此函数后，可以将指针 A_fft 和 B_fft 强制转换为 bfp_s32_t* 来访问时域信号。

操作： a[n]=∑f=0N/2−1(A[f]⋅ej2πfn/N)，其中 0≤n<Na[n] = \sum_{f=0}^{N/2-1} \left( A[f]\cdot e^{j2\pi fn/N} \right) \text{，其中 } 0 \le n < N

b[n]=∑f=0N/2−1(B[f]⋅ej2πfn/N)，其中 0≤n<Nb[n] = \sum_{f=0}^{N/2-1} \left( B[f]\cdot e^{j2\pi fn/N} \right) \text{，其中 } 0 \le n < N

示例：

// 使用样本初始化时域数据。
int32_t bufferA[N] = { ... };
int32_t bufferB[N] = { ... };
complex_s32_t scratch[N]; // 临时缓冲区 - 内容不重要
bfp_s32_t channel_A, channel_B;
bfp_s32_init(&channel_A, buffer, 0, N, 1);
bfp_s32_init(&channel_B, buffer, 0, N, 1);

// 执行正向DFT
bfp_fft_forward_stereo(&channel_A, &channel_B, scratch);
      
// channel_A 和 channel_B 现在应被视为已修改，因为结构体现在实际上是 bfp_complex_s32_t
bfp_complex_s32_t* chanA = (bfp_complex_s32_t*) &channel_A;
bfp_complex_s32_t* chanB = (bfp_complex_s32_t*) &channel_B;

// 使用 `chanA` 和 `chanB` 对频域数据进行操作
...
// 执行逆DFT以返回时域
bfp_fft_inverse_stereo(&chanA, &chanB, scratch);
      
// 再次使用 channel_A 和 channel_B 来使用新的时域数据
...

参数：

  • bfp_complex_s32_t *A_fft – [inout] [out] 频域BFP向量 Aˉ\bar A。[out] 时域BFP向量 aˉ\bar a
  • bfp_complex_s32_t *B_fft – [inout] [out] 频域BFP向量 Bˉ\bar B。[out] 时域BFP向量 bˉ\bar b
  • complex_s32_t scratch[] – 至少包含 2*A_fft->length 个 complex_s32_t 元素的临时缓冲区

参考性能:

bfp_fft_inverse_stereo

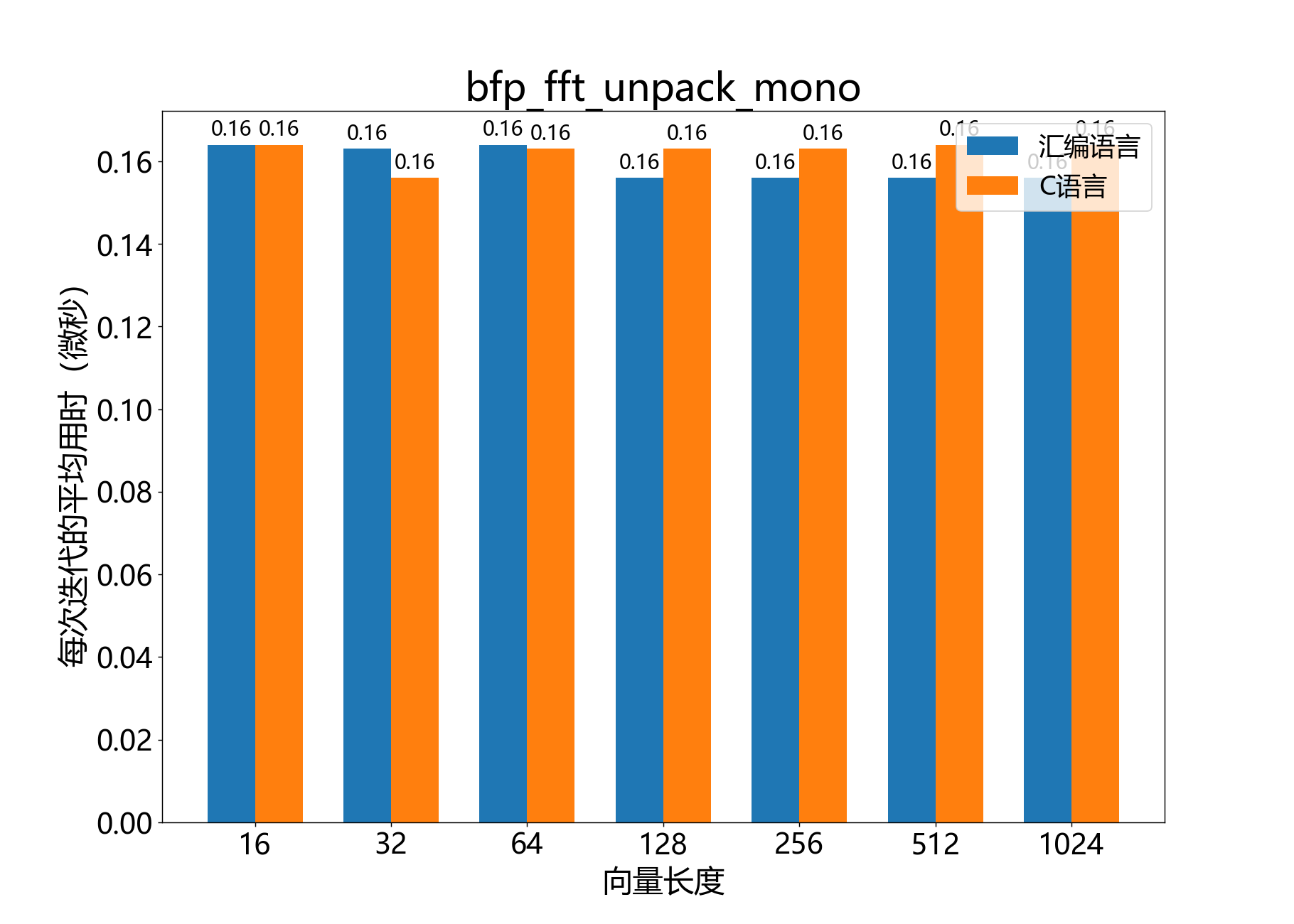
void bfp_fft_unpack_mono()​

解包由 bfp_fft_forward_mono() 得到的频谱。

实数信号的DFT以FFT_N（FFT长度）为周期，并在索引0处具有复共轭对称性。这两个属性保证了频谱的DC分量（索引0）和Nyquist分量（索引FFT_N/2）的虚部都是零。为了在原地计算正向FFT，bfp_fft_forward_mono()将输出频谱的Nyquist速率分量的实部打包到DC分量的虚部。

当对信号的复频谱进行操作时，这可能是不希望的。使用此函数来解包Nyquist分量。此函数还会调整BFP向量的长度以反映此解包。

**注意：**如果你打算使用此函数解包频谱，时域BFP向量的缓冲区长度必须为FFT_N+2，而不是FFT_N（int32_t元素），但这些不应反映在时域BFP向量的length字段中。

操作：

Re{xN/2}←Im{x0}Im{x0}←0Im{xN/2}←0x.length←x.length+1\begin{split}\begin{align*} & Re\{x_{N/2}\} && \leftarrow Im\{x_0\} \\ & Im\{x_0\} && \leftarrow 0 \\ & Im\{x_{N/2}\} && \leftarrow 0 \\ & x.length && \leftarrow x.length + 1 \end{align*}\end{split}

**注意：**在应用bfp_fft_inverse_mono()之前，必须调用bfp_fft_pack_mono()，因为逆FFT期望数据被打包。

参数：

  • bfp_complex_s32_t *x – [输入/输出] 需要解包的频谱

参见： bfp_fft_forward_mono, bfp_fft_pack_mono

参考性能:

bfp_fft_unpack_mono

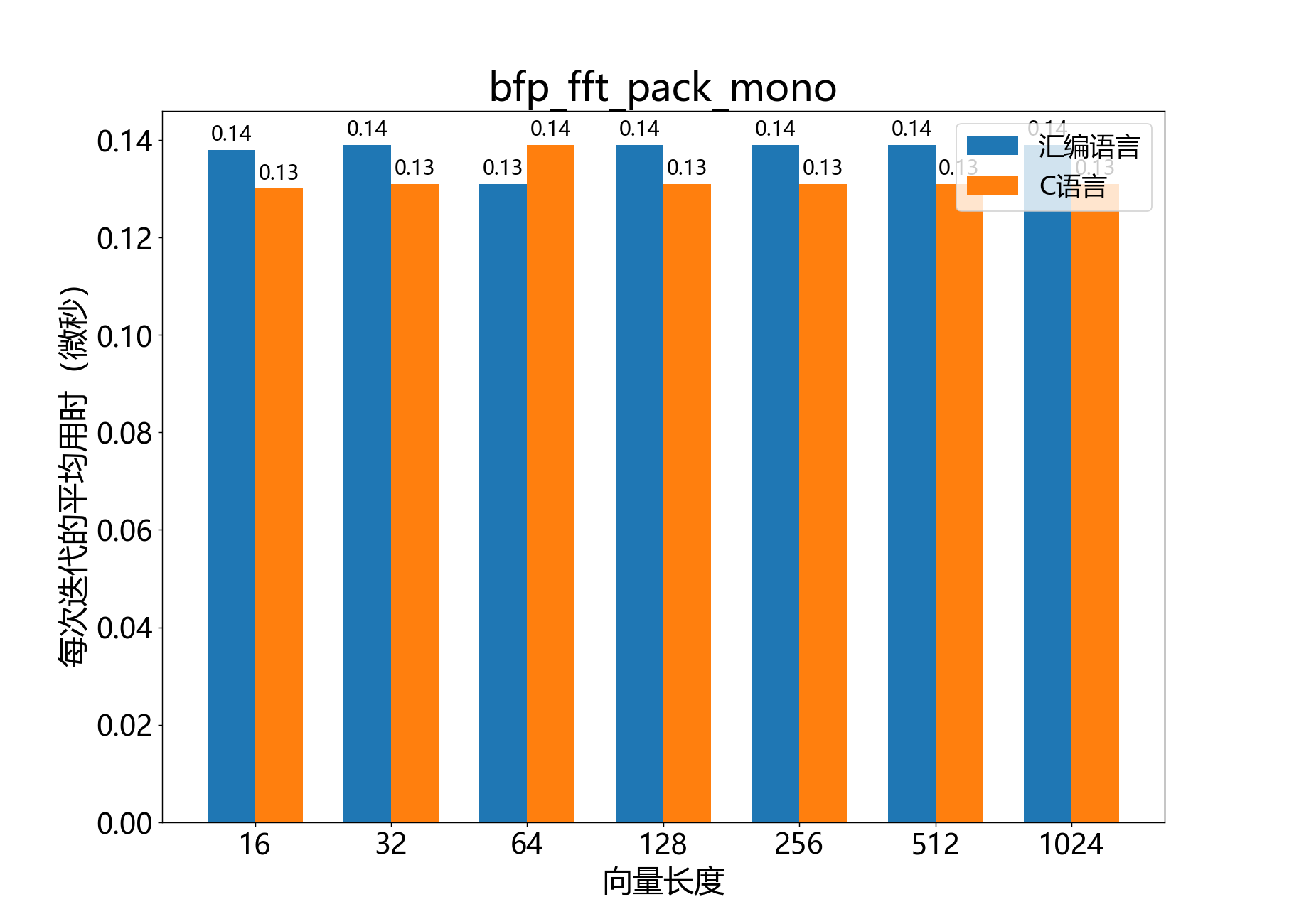
void bfp_fft_pack_mono()​

打包由 bfp_fft_unpack_mono() 得到的频谱。

此函数应用bfp_fft_unpack_mono()的反转过程，为使用bfp_fft_inverse_mono()进行逆FFT做准备。

参数：

  • bfp_complex_s32_t *x – [输入/输出] 需要打包的频谱

参见： bfp_fft_inverse_mono, bfp_fft_unpack_mono

参考性能:

bfp_fft_pack_mono

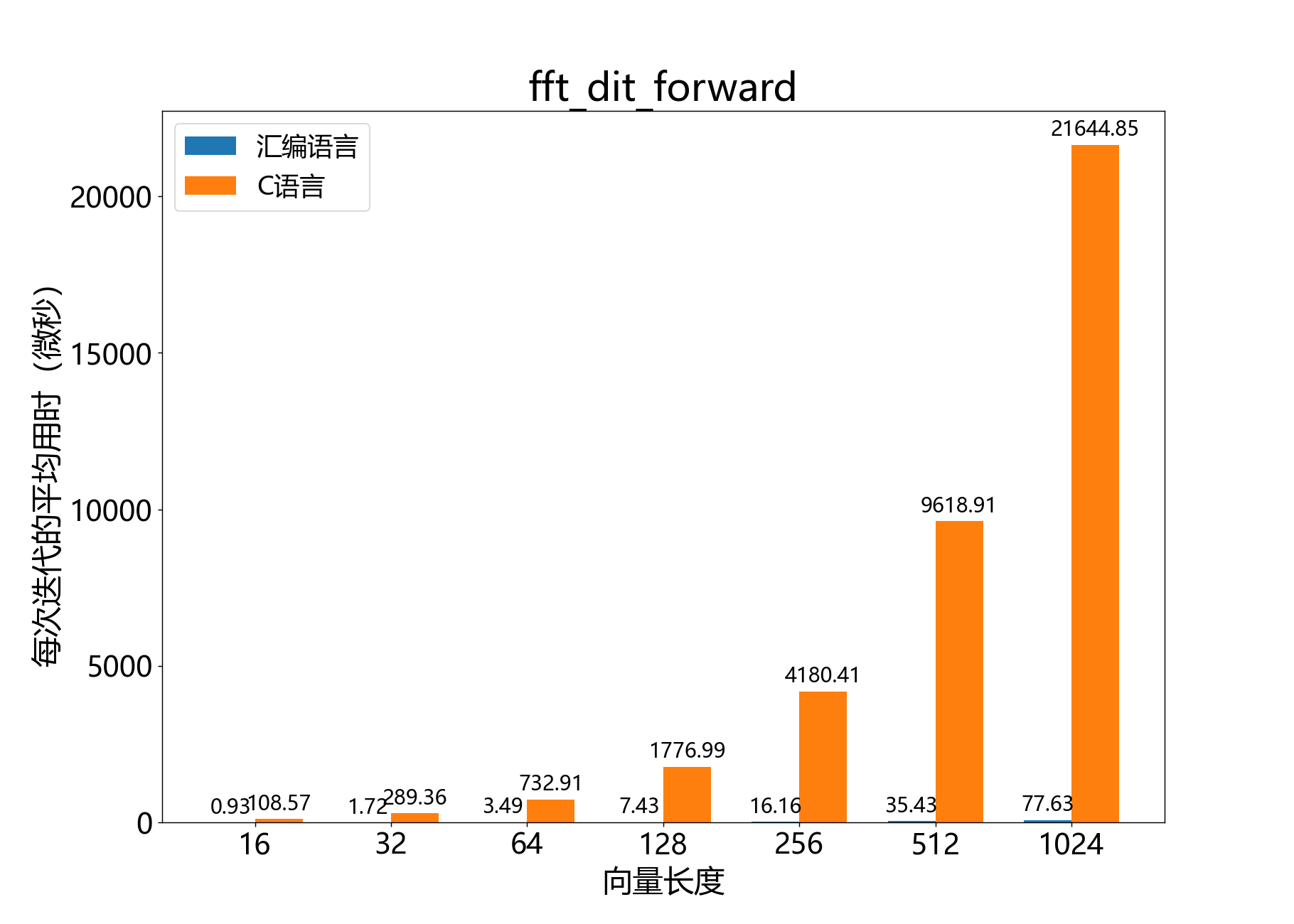
void fft_dit_forward()​

使用时间抽取FFT算法计算正向DFT。

此函数使用时间抽取FFT算法计算复数输入信号的N点正向DFT。结果在原地计算。

操作： X[f]=12α∑n=0N−1(x[n]⋅e−j2πfn/N) for 0≤f<NX[f] = \frac{1}{2^{\alpha}} \sum_{n=0}^{N-1} \left( x[n]\cdot e^{-j2\pi fn/N} \right) \text{ for } 0 \le f < N

x[]被解释为一个具有共享指数*exp和在x[]中初始头空间*hr的块浮点向量。在计算过程中，此函数会监视数据的头空间，并通过适当地将数据向上或向下位移来补偿，以避免溢出和下溢。在上面的等式中，α\alpha表示数据被右移的（净）位数。

完成后，*hr将更新为x[]中的最终头空间，指数*exp将增加α\alpha。

备注

为了保证不会发生饱和，x[]必须至少有2位的_初始_头空间。

参数：

  • complex_s32_t x[] – [输入/输出] 要被转换的N元素复数输入向量。
  • const unsigned N – [out] 要执行的DFT的大小。
  • headroom_t* hr – [输入/输出] 指向x[]中初始头空间的指针。
  • exponent_t* exp – [输入/输出] 指向与x[]相关联的初始指数的指针。

异常： ET_LOAD_STORE 如果x未字对齐（参见 @ref note_vector_alignment）

参考性能:

fft_dit_forward

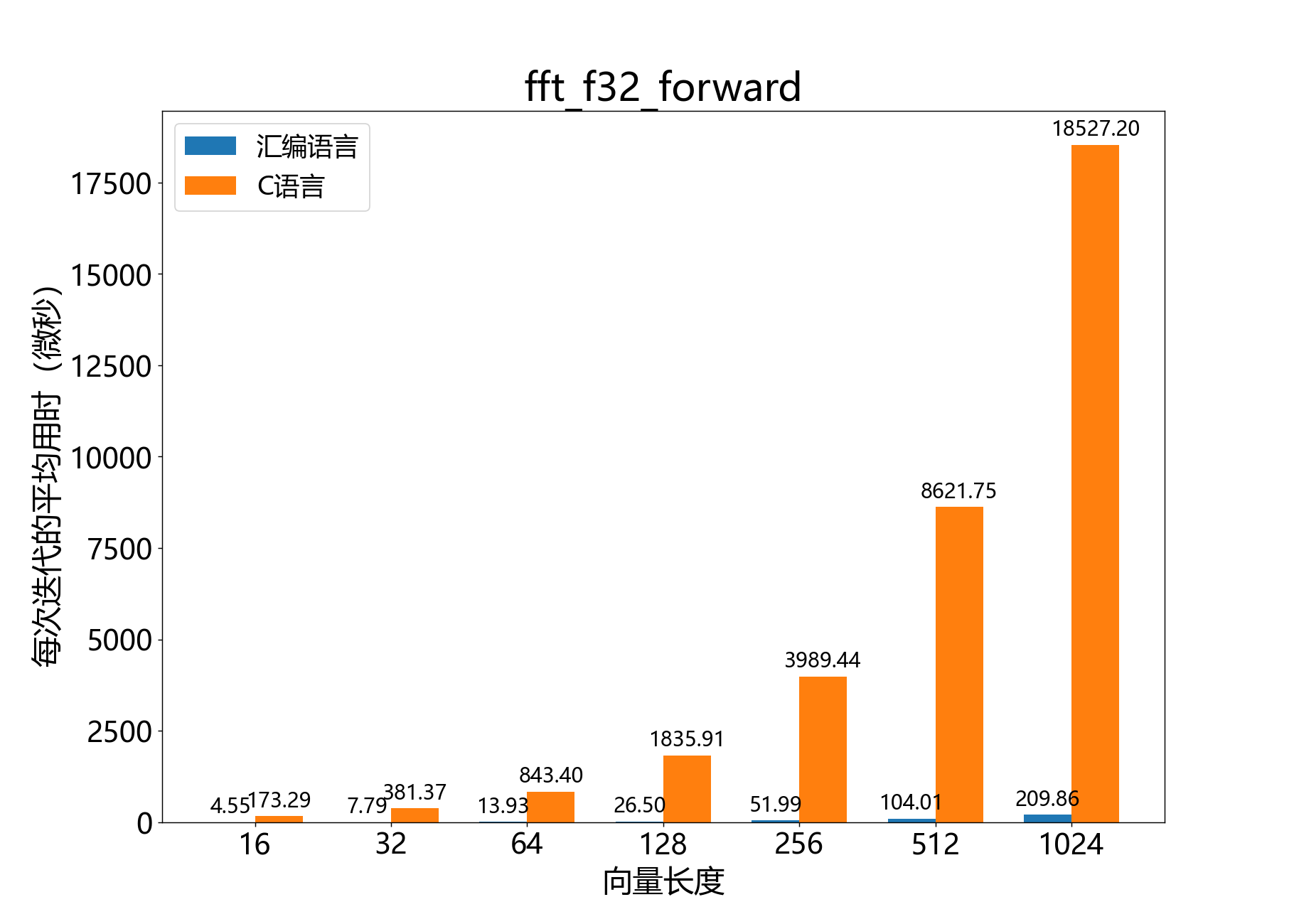
complex_float_t* fft_f32_forward()​

对IEEE754浮点数向量执行正向FFT。

该函数接受实数输入向量xˉ\bar{x}，并在原地对信号执行正向FFT，得到输出向量Xˉ=FFT{xˉ}\bar{X} = FFT\{\bar{x}\}。这个实现通过将IEEE754浮点数向量转换为块浮点数表示来加速FFT的计算。然后将结果BFP频谱转换回IEEE754单精度浮点数。该操作在x[]上进行原地操作。

具体的FFT细节请参考bfp_fft_forward_mono()函数。

输入x[]是一个由fft_length个float元素组成的数组，输出（放在x[]中）是一个由fft_length/2个complex_float_t元素组成的数组，所以应该在调用此函数后进行类型转换。

const unsigned FFT_N = 512
float time_series[FFT_N] = { ... };
fft_f32_forward(time_series, FFT_N);
complex_float_t* freq_spectrum = (complex_float_t*) &time_series[0];
const unsigned FREQ_BINS = FFT_N/2;
// 例如：freq_spectrum[FREQ_BINS-1].re

x[]必须从双字对齐的地址开始。

操作：

Xˉ←FFT{xˉ}\bar{X} \leftarrow FFT\{\bar{x}\}

参数：

  • float x[] – [输入/输出] 输入向量 xˉ\bar{x}

  • const unsigned fft_length – [out] 向量 xˉ\bar{x}的长度

返回值：

  • 指向频域频谱的指针（即 ((complex_float_t*) &x[0])）

异常：

  • ET_LOAD_STORE 如果x没有双字对齐（参见@ref note_vector_alignment）则抛出此异常

参考性能:

fft_f32_forward

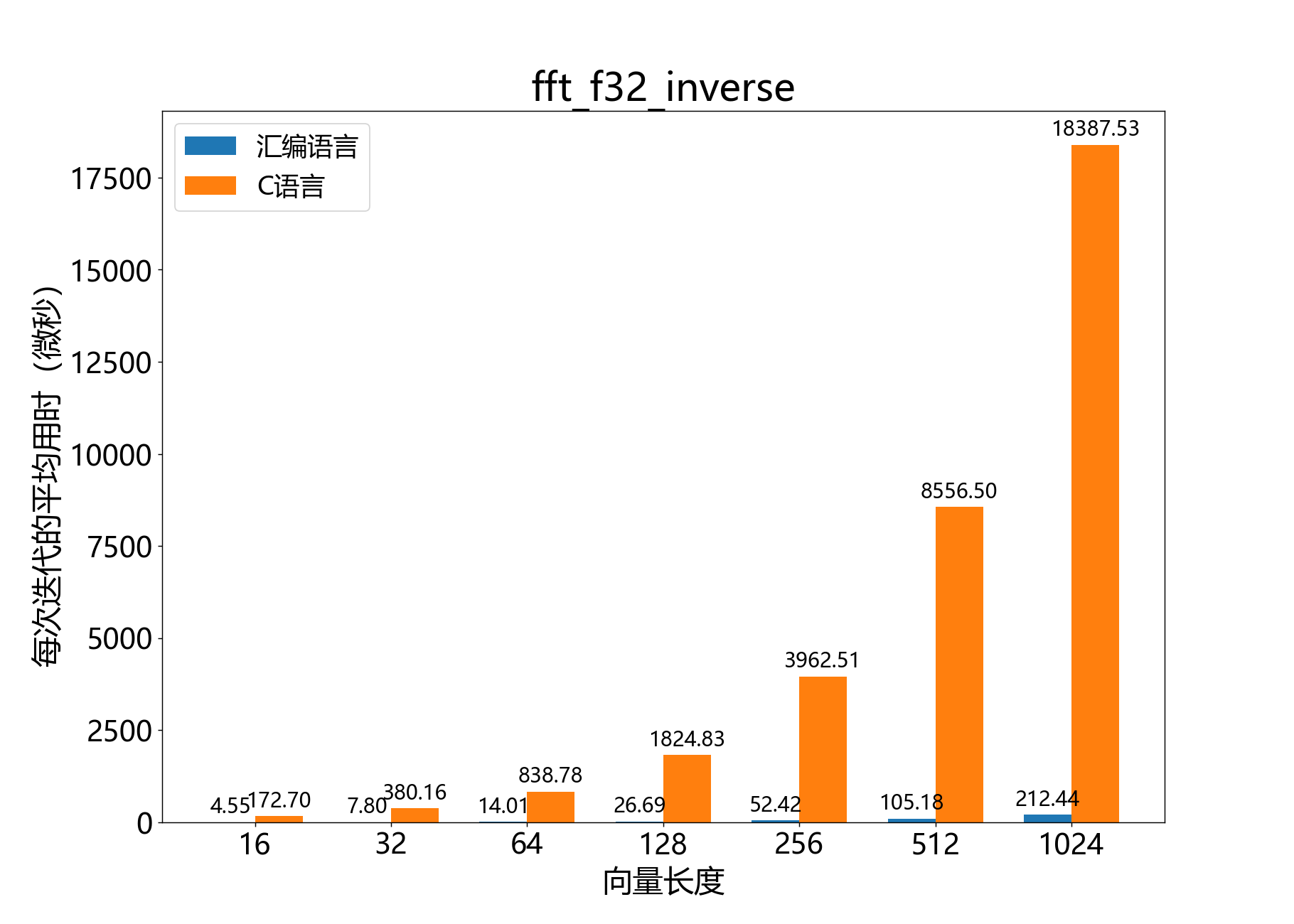
float* fft_f32_inverse()​

对complex_float_t向量进行逆FFT。

该函数接受复数输入向量Xˉ\bar{X}，并在原地对频谱执行逆实数FFT，得到输出向量xˉ=IFFT{Xˉ}\bar{x} = IFFT\{\bar{X}\}。这个实现通过将IEEE754浮点数向量转换为块浮点数表示来加速IFFT的计算。然后将结果BFP信号转换回IEEE754单精度浮点数。该操作在X[]上进行原地操作。

具体的IFFT细节请参考bfp_fft_inverse_mono()函数。

输入X[]是一个由fft_length/2个complex_float_t元素组成的数组。输出（放在X[]中）是一个由fft_length个float元素组成的数组。

const unsigned FFT_N = 512
complex_float_t freq_spectrum[FFT_N/2] = { ... };
fft_f32_inverse(freq_spectrum, FFT_N);
float* time_series = (float*) &freq_spectrum[0];

X[]必须从双字对齐的地址开始。

参数：

  • complex_float_t X[] – [输入/输出] 输入向量 Xˉ\bar{X}

  • const unsigned fft_length – [out] FFT长度。是Xˉ\bar{X}的元素数量的两倍。

返回值：

  • 指向时域信号的指针（即 ((float*) &X[0])）

异常：

  • ET_LOAD_STORE 如果X没有双字对齐（参见@ref note_vector_alignment）则抛出此异常

参考性能:

fft_f32_inverse

编辑此页
本文最后由 Vergil Wong 更新于