第2B部分：尝试双发射（dual-issue）汇编优化

与第2A部分类似，第2B部分使用定点算术实现了FIR滤波器。

在第2A部分中，我们直接在普通C中实现了定点算术。因此，我们只能希望编译器生成一系列高效的指令来完成工作。然而，有理由怀疑编译器是否生成了最优的实现。

一个原因是C编译器在编译代码时不会针对VPU进行优化。另一个原因是编译器通常不会生成使用C编写的函数的双发射（dual-issue）实现。

在第2B部分中，我们不是在普通的C循环中实现逻辑，而是使用一个双发射（dual-issue）汇编函数来计算内积。这个函数int32_dot()不使用VPU（我们将在下一阶段使用VPU），但是它旨在展示仅仅使用直接编写的汇编双发射（dual-issue）函数就能获得的性能改进。

实现

在这一部分中，filter_task()、rx_frame()和tx_frame()与第2A部分中的相同。

src/part2B/part2B.c

//将滤波器应用于生成单个输出样本
q1_31 filter_sample(
    const q1_31 sample_history[TAP_COUNT])
{
  // 与滤波器系数关联的指数
  const exponent_t coef_exp = -28;
  // 与输入信号关联的指数
  const exponent_t input_exp = -31;
  // 与输出信号关联的指数
  const exponent_t output_exp = input_exp;
  // 与累加器关联的指数
  const exponent_t acc_exp = input_exp + coef_exp;
  // 应用于滤波器累加器的算术右移，以达到正确的输出指数
  const right_shift_t acc_shr = output_exp - acc_exp;

  // 计算样本历史和滤波器系数之间的64位内积
  int64_t acc = int32_dot(&sample_history[0], 
                          &filter_coef[0], 
                          TAP_COUNT);

  // 应用右移，将位深度降至32位
  return ashr64(acc, acc_shr);
}

注意，与第2A部分相比，唯一的区别是调用了int32_dot()，而不是使用循环。

/**
 * 计算两个32位整数向量之间的64位内积。
 * 
 * 此函数在`int32_dot.S`中直接以汇编实现。
 * 
 * 此函数经过优化，但仅使用标量算术单元，不使用VPU。
 */
int64_t int32_dot(
    const int32_t x[],
    const int32_t y[],
    const unsigned length);

int32_dot()接受两个长度为length的int32_t数组，并计算直接内积作为int64_t输出。即

$$\mathtt{int32\_dot} \to \sum_{k=0}^{\mathtt{length}-1} {\mathtt{x}[k] \cdot \mathtt{y}[k]}$$

如果你感兴趣，可以查看int32_dot.S中的实现。

需要指出的一点是int32_dot.S的内部循环（从.L_loop_top:到.L_loop_bot:）只有4条指令长。对第2A部分固件进行反汇编（xobjdump -D bin/stage3.xe）可以看到，在这种情况下，第2A部分中（单发射）filter_frame()的内部循环有7条指令长。

结果

第2B部分的执行时间与第2A部分的执行时间之比几乎为(4/7)。

时间

时间类型	测量时间
每个滤波器系数	33.62 ns
每个输出样本	34425.00 ns
每帧	8881434.00 ns

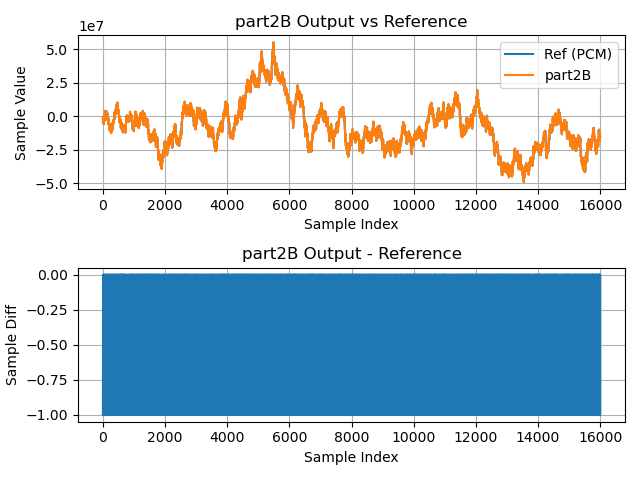
输出波形图