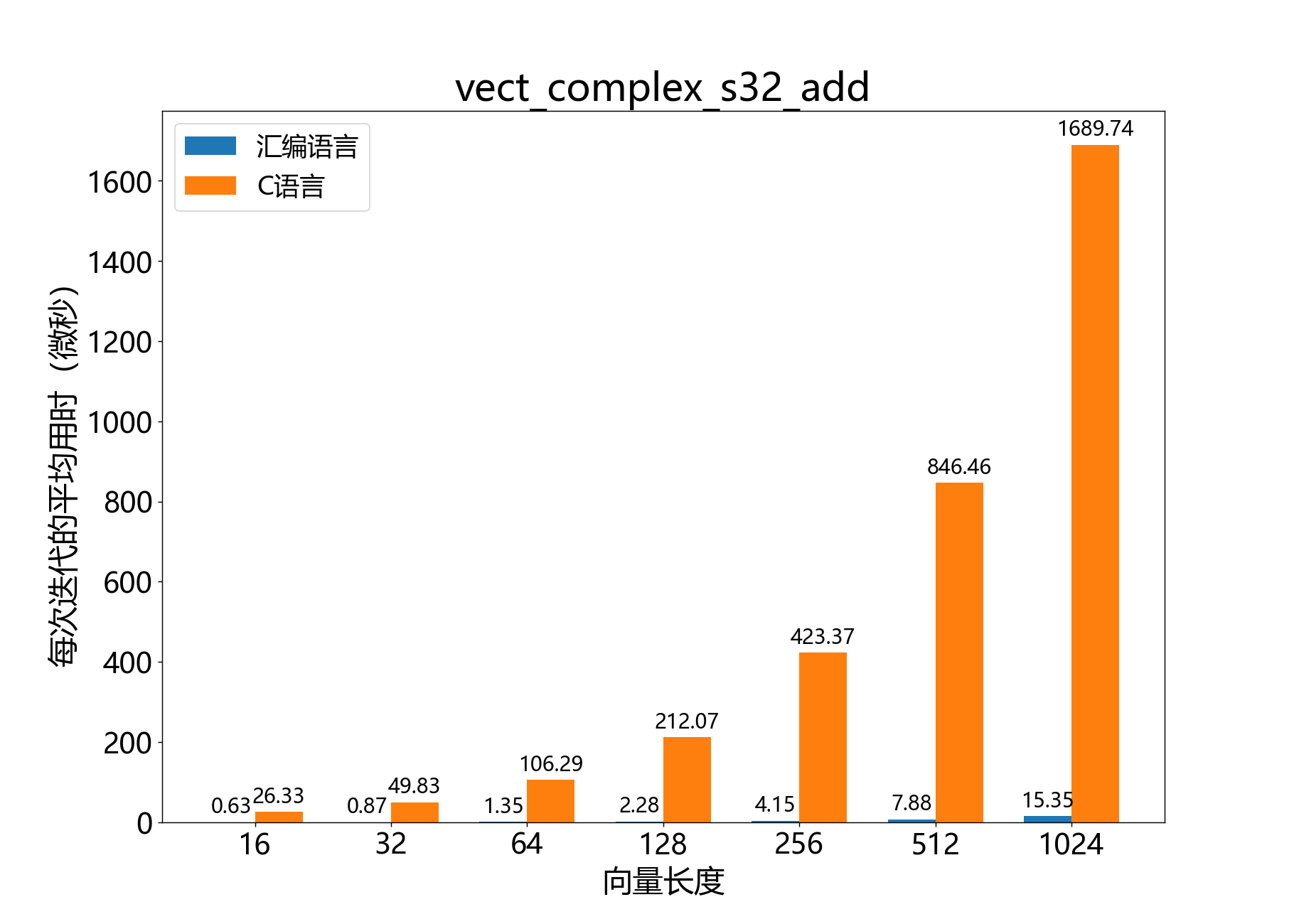
Complex 32-bit Vector API headroom_t vect_complex_s32_add() 将一个复数32位向量与另一个相加。
a[]、b[]和c[]分别表示复数32位尾数向量 a ˉ \bar{a} a ˉ b ˉ \bar{b} b ˉ c ˉ \bar{c} c ˉ b[]或c[]上安全地原地执行。
length是每个向量中的元素数量。
b_shr和c_shr是应用于 b ˉ \bar{b} b ˉ c ˉ \bar{c} c ˉ
操作:
b k ′ ← s a t 32 ( ⌊ b k ⋅ 2 − b _ s h r ⌋ ) c k ′ ← s a t 32 ( ⌊ c k ⋅ 2 − c _ s h r ⌋ ) R e { a k } ← R e { b k ′ } + R e { c k ′ } I m { a k } ← I m { b k ′ } + I m { c k ′ } 其中 k �∈ 0 . . . ( l e n g t h − 1 ) \begin{align*}
&b_k' \leftarrow sat_{32}(\lfloor b_k \cdot 2^{-b\_shr} \rfloor) \\
&c_k' \leftarrow sat_{32}(\lfloor c_k \cdot 2^{-c\_shr} \rfloor) \\
&Re\{a_k\} \leftarrow Re\{b_k'\} + Re\{c_k'\} \\
&Im\{a_k\} \leftarrow Im\{b_k'\} + Im\{c_k'\} \\
&\text{其中 }k\in 0\ ...\ (length-1)
\end{align*} b k ′ ← s a t 32 (⌊ b k ⋅ 2 − b _ s h r ⌋) c k ′ ← s a t 32 (⌊ c k ⋅ 2 − c _ s h r ⌋) R e { a k } ← R e { b k ′ } + R e { c k ′ } I m { a k } ← I m { b k ′ } + I m { c k ′ } 其中 k ∈ 0 ... ( l e n g t h − 1 ) 块浮点数:
如果 b ˉ \bar{b} b ˉ c ˉ \bar{c} c ˉ b ˉ ⋅ 2 b _ e x p \bar{b} \cdot 2^{b\_exp} b ˉ ⋅ 2 b _ e x p c ˉ ⋅ 2 c _ e x p \bar{c} \cdot 2^{c\_exp} c ˉ ⋅ 2 c _ e x p a ˉ \bar{a} a ˉ a ˉ ⋅ 2 a _ e x p \bar{a} \cdot 2^{a\_exp} a ˉ ⋅ 2 a _ e x p
在这种情况下,必须选择 b _ s h r b\_shr b _ s h r c _ s h r c\_shr c _ s h r a _ e x p = b _ e x p + b _ s h r = c _ e x p + c _ s h r a\_exp = b\_exp + b\_shr = c\_exp + c\_shr a _ e x p = b _ e x p + b _ s h r = c _ e x p + c _ s h r
函数vect_complex_s32_add_prepare()可以根据输入指数 b _ e x p b\_exp b _ e x p c _ e x p c\_exp c _ e x p b _ h r b\_hr b _ h r c _ h r c\_hr c _ h r a _ e x p a\_exp a _ e x p b _ s h r b\_shr b _ s h r c _ s h r c\_shr c _ s h r
参数:
complex_s32_t a[] – [out]a ˉ \bar{a} a ˉ
const complex_s32_t b[] – [in]b ˉ \bar{b} b ˉ
const complex_s32_t c[] – [in]c ˉ \bar{c} c ˉ
const unsigned length – [in]a ˉ \bar{a} a ˉ b ˉ \bar{b} b ˉ c ˉ \bar{c} c ˉ
const right_shift_t b_shr – [in]b ˉ \bar{b} b ˉ
const right_shift_t c_shr – [in]c ˉ \bar{c} c ˉ
返回值:
异常:
ET_LOAD_STOREa、b或c不是字对齐的,则引发异常(参见 笔记:向量对齐 )
另请参阅:
vect_complex_s32_add_prepare
参考性能 :
headroom_t vect_complex_s32_add_scalar() 将一个标量加到复数32位向量中。
该操作将复数标量加到复数32位向量的每个元素上。该操作可以在输入向量上安全地原地执行。
操作:
b k ′ ← s a t 32 ( ⌊ b k ⋅ 2 − b _ s h r ⌋ ) R e { a k } ← R e { b k ′ } + R e { c } I m { a k } ← I m { b k ′ } + I m { c } 其中 k ∈ 0 . . . ( l e n g t h − 1 ) \begin{align*}
& b_k' \leftarrow sat_{32}(\lfloor b_k \cdot 2^{-b\_shr} \rfloor) \\
& Re\{a_k\} \leftarrow Re\{b_k'\} + Re\{c\} \\
& Im\{a_k\} \leftarrow Im\{b_k'\} + Im\{c\} \\
& \qquad\text{ 其中 }k\in 0\ ...\ (length-1)
\end{align*} b k ′ ← s a t 32 (⌊ b k ⋅ 2 − b _ s h r ⌋) R e { a k } ← R e { b k ′ } + R e { c } I m { a k } ← I m { b k ′ } + I m { c } 其中 k ∈ 0 ... ( l e n g t h − 1 ) 参数:
complex_s32_t a[] – [out]a ˉ \bar{a} a ˉ
const complex_s32_t b[] – [in]b ˉ \bar{b} b ˉ
const complex_s32_t c – [in]c c c
const unsigned length – [in]a ˉ \bar{a} a ˉ b ˉ \bar{b} b ˉ
const right_shift_t b_shr – [in]b ˉ \bar{b} b ˉ
返回值:
异常:
ET_LOAD_STORE 如果 a 或 b 不是字对齐的(参见 笔记:向量对齐 )
另请参阅:
vect_complex_s32_add_scalar_prepare
参考性能 :
headroom_t vect_complex_s32_conj_mul() 逐元素将一个复数32位向量与另一个复数的共轭相乘。
该操作对一个复数32位向量与另一个复数的共轭进行逐元素相乘。该操作可以在输入向量上安全地原地执行。
操作:
b k ′ ← s a t 32 ( ⌊ b k ⋅ 2 − b _ s h r ⌋ ) c k ′ ← s a t 32 ( ⌊ c k ⋅ 2 − c _ s h r ⌋ ) R e { a k } ← ( R e { b k ′ } ⋅ R e { c k ′ } + I m { b k ′ } ⋅ I m { c k ′ } ) ⋅ 2 − 30 I m { a k } ← ( I m { b k ′ } ⋅ R e { c k ′ } − R e { b k ′ } ⋅ I m { c k ′ } ) ⋅ 2 − 30 其中 k ∈ 0 . . . ( l e n g t h − 1 ) \begin{align*}
& b_k' \leftarrow sat_{32}(\lfloor b_k \cdot 2^{-b\_shr} \rfloor) \\
& c_k' \leftarrow sat_{32}(\lfloor c_k \cdot 2^{-c\_shr} \rfloor) \\
& Re\{a_k\} \leftarrow \left( Re\{b_k'\} \cdot Re\{c_k'\} + Im\{b_k'\} \cdot Im\{c_k'\} \right) \cdot 2^{-30} \\
& Im\{a_k\} \leftarrow \left( Im\{b_k'\} \cdot Re\{c_k'\} - Re\{b_k'\} \cdot Im\{c_k'\} \right) \cdot 2^{-30} \\
& \qquad\text{ 其中 }k\in 0\ ...\ (length-1)
\end{align*} b k ′ ← s a t 32 (⌊ b k ⋅ 2 − b _ s h r ⌋) c k ′ ← s a t 32 (⌊ c k ⋅ 2 − c _ s h r ⌋) R e { a k } ← ( R e { b k ′ } ⋅ R e { c k ′ } + I m { b k ′ } ⋅ I m { c k ′ } ) ⋅ 2 − 30 I m { a k } ← ( I m { b k ′ } ⋅ R e { c k ′ } − R e { b k ′ } ⋅ I m { c k ′ } ) ⋅ 2 − 30 其中 k ∈ 0 ... ( l e n g t h − 1 ) 参数:
complex_s32_t a[] – [out]a ˉ \bar{a} a ˉ
const complex_s32_t b[] – [in]b ˉ \bar{b} b ˉ
const complex_s32_t c[] – [in]c ˉ \bar{c} c ˉ
const unsigned length – [in]a ˉ \bar{a} a ˉ b ˉ \bar{b} b ˉ c ˉ \bar{c} c ˉ
const right_shift_t b_shr – [in]b ˉ \bar{b} b ˉ
const right_shift_t c_shr – [in]c ˉ \bar{c} c ˉ
返回值:
异常:
ET_LOAD_STORE �如果 a、b 或 c 不是字对齐的(参见 笔记:向量对齐 )
另请参阅:
vect_complex_s32_conj_mul_prepare
参考性能 :
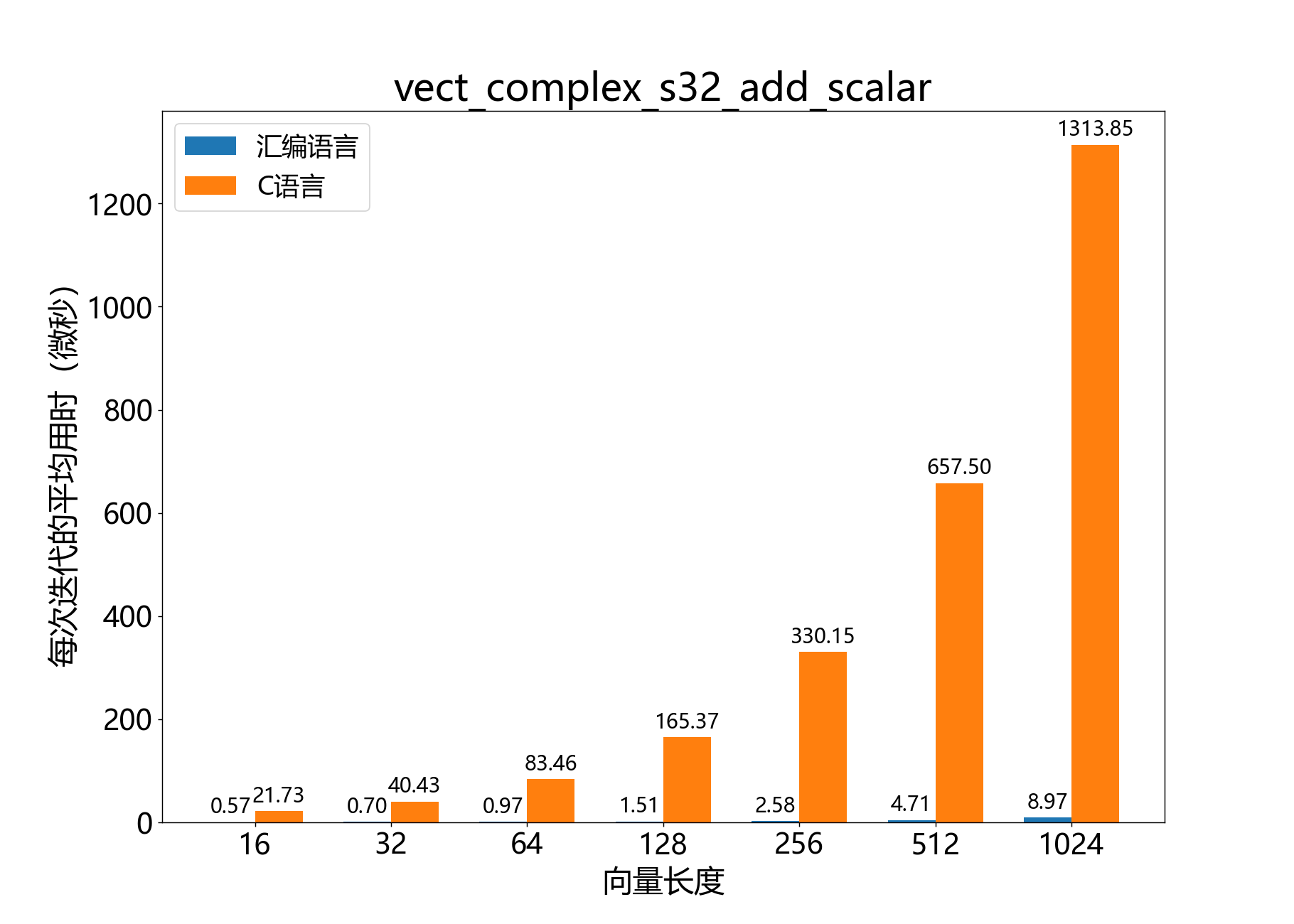
headroom_t vect_complex_s32_add_scalar() 将一个标量加到复数32位向量中。
该操作将复数标量加到复数32位向量的每个元素上。该操作可以在输入向量上安全地原地执行。
操作:
b k ′ ← s a t 32 ( ⌊ b k ⋅ 2 − b _ s h r ⌋ ) R e { a k } ← R e { b k ′ } + R e { c } I m { a k } ← I m { b k ′ } + I m { c } 其中 k ∈ 0 . . . ( l e n g t h − 1 ) \begin{align*}
& b_k' \leftarrow sat_{32}(\lfloor b_k \cdot 2^{-b\_shr} \rfloor) \\
& Re\{a_k\} \leftarrow Re\{b_k'\} + Re\{c\} \\
& Im\{a_k\} \leftarrow Im\{b_k'\} + Im\{c\} \\
& \qquad\text{ 其中 }k\in 0\ ...\ (length-1)
\end{align*} b k ′ ← s a t 32 (⌊ b k ⋅ 2 − b _ s h r ⌋) R e { a k } ← R e { b k ′ } + R e { c } I m { a k } ← I m { b k ′ } + I m { c } 其中 k ∈ 0 ... ( l e n g t h − 1 ) 参数:
complex_s32_t a[] – [out]a ˉ \bar{a} a ˉ
const complex_s32_t b[] – [in]b ˉ \bar{b} b ˉ
const complex_s32_t c – [in]c c c
const unsigned length – [in]a ˉ \bar{a} a ˉ b ˉ \bar{b} b ˉ
const right_shift_t b_shr – [in]b ˉ \bar{b} b ˉ
返回值:
异常:
ET_LOAD_STORE 如果 a 或 b 不是字对齐的(参见 笔记:向量对齐 )
另请参阅:
vect_complex_s32_add_scalar_prepare
参考性能 :
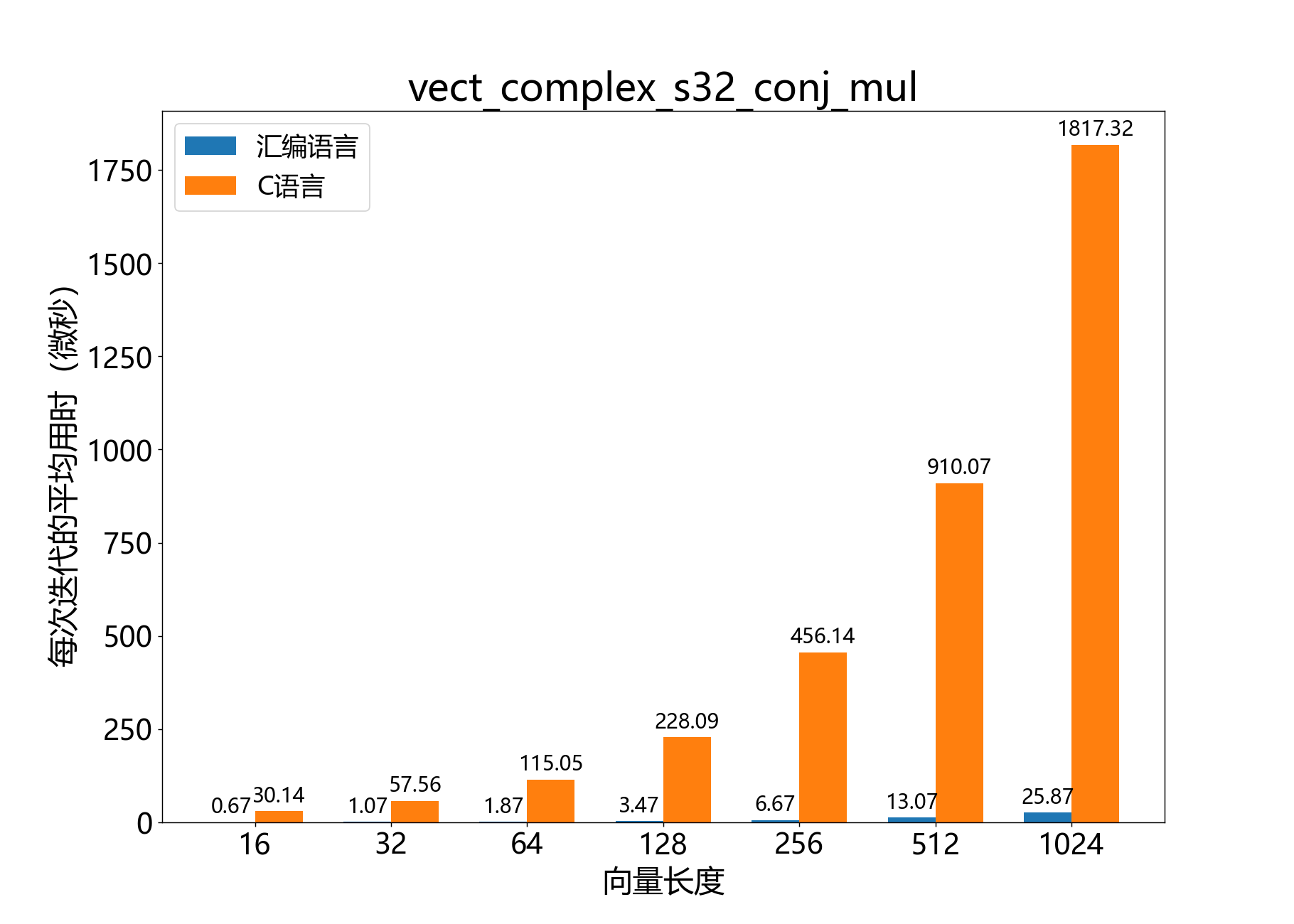
headroom_t vect_complex_s32_conj_mul() 逐元素将一个复数32位向量与另一个复数的共轭相乘。
该操作对一个复数32位向量与另一个复数的共轭进行逐元素相乘。该操作可以在输入向量上安全地原地执行。
操作:
b k ′ ← s a t 32 ( ⌊ b k ⋅ 2 − b _ s h r ⌋ ) c k ′ ← s a t 32 ( ⌊ c k ⋅ 2 − c _ s h r ⌋ ) R e { a k } ← ( R e { b k ′ } ⋅ R e { c k ′ } + I m { b k ′ } ⋅ I m { c k ′ } ) ⋅ 2 − 30 I m { a k } ← ( I m { b k ′ } ⋅ R e { c k ′ } − R e { b k ′ } ⋅ I m { c k ′ } ) ⋅ 2 − 30 其中 k ∈ 0 . . . ( l e n g t h − 1 ) \begin{align*}
& b_k' \leftarrow sat_{32}(\lfloor b_k \cdot 2^{-b\_shr} \rfloor) \\
& c_k' \leftarrow sat_{32}(\lfloor c_k \cdot 2^{-c\_shr} \rfloor) \\
& Re\{a_k\} \leftarrow \left( Re\{b_k'\} \cdot Re\{c_k'\} + Im\{b_k'\} \cdot Im\{c_k'\} \right) \cdot 2^{-30} \\
& Im\{a_k\} \leftarrow \left( Im\{b_k'\} \cdot Re\{c_k'\} - Re\{b_k'\} \cdot Im\{c_k'\} \right) \cdot 2^{-30} \\
& \qquad\text{ 其中 }k\in 0\ ...\ (length-1)
\end{align*} b k ′ ← s a t 32 (⌊ b k ⋅ 2 − b _ s h r ⌋) c k ′ ← s a t 32 (⌊ c k ⋅ 2 − c _ s h r ⌋) R e { a k } ← ( R e { b k ′ } ⋅ R e { c k ′ } + I m { b k ′ } ⋅ I m { c k ′ } ) ⋅ 2 − 30 I m { a k } ← ( I m { b k ′ } ⋅ R e { c k ′ } − R e { b k ′ } ⋅ I m { c k ′ } ) ⋅ 2 − 30 其中 k ∈ 0 ... ( l e n g t h − 1 ) 参数:
complex_s32_t a[] – [out]a ˉ \bar{a} a ˉ
const complex_s32_t b[] – [in]b ˉ \bar{b} b ˉ
const complex_s32_t c[] – [in]c ˉ \bar{c} c ˉ
const unsigned length – [in]a ˉ \bar{a} a ˉ b ˉ \bar{b} b ˉ c ˉ \bar{c} c ˉ
const right_shift_t b_shr – [in]b ˉ \bar{b} b ˉ
const right_shift_t c_shr – [in]c ˉ \bar{c} c ˉ
返回值:
异常:
ET_LOAD_STORE 如果 a、b 或 c 不是字对齐的(参见 笔记:向量对齐 )
另请参阅:
vect_complex_s32_conj_mul_prepare
参考性能 :
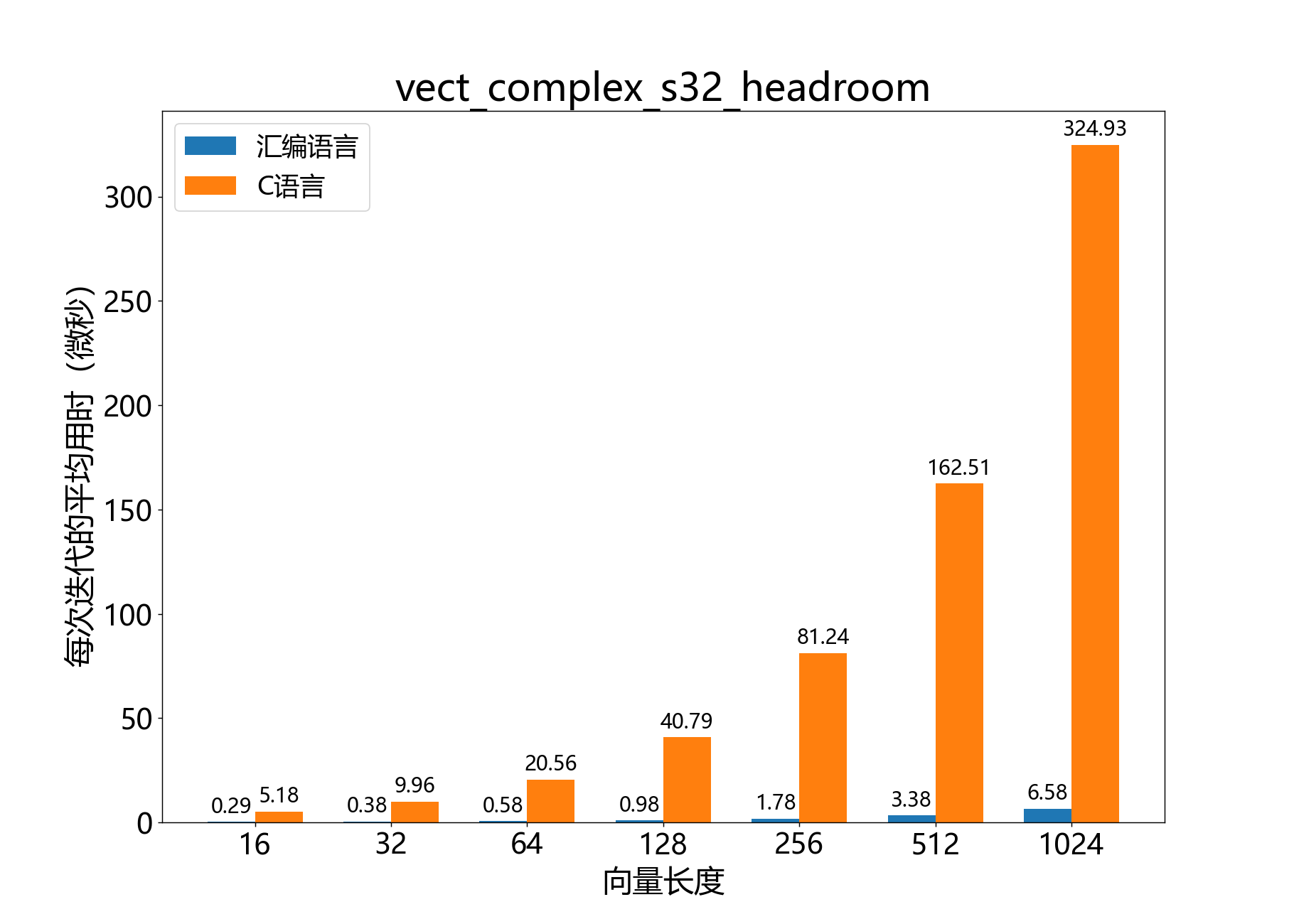
headroom_t vect_complex_s32_headroom() 计算复数32位数组的头空间。
N位整数的头空间是整数的值可以左移的位数,而不会丢失任何信息。等效地说,它比前导符号位的数量少1。
complex_s32_t结构体的头空间是其32位字段re和im的头空间的最小值。
complex_s32_t数组的头空间是其每个complex_s32_t元素的头空间的最小值。
该函数有效地遍历元素x ˉ \bar{x} x ˉ
x[]表示复数32位向量x ˉ \bar{x} x ˉ x[]必须从字对齐的地址开始。
length是x[]中的元素数量。
操作定义为:
m i n { H R 32 ( x 0 ) , H R 32 ( x 1 ) , . . . , H R 32 ( x l e n g t h − 1 ) } min\!\{ HR_{32}\left(x_0\right), HR_{32}\left(x_1\right), ..., HR_{32}\left(x_{length-1}\right) \} min { H R 32 ( x 0 ) , H R 32 ( x 1 ) , ... , H R 32 ( x l e n g t h − 1 ) } 参数:
返回值:
异常:
如果x不是字对齐的,则引发ET_LOAD_STORE异常(参见 笔记:向量对齐 )
另请参阅:
vect_s16_headroom,
vect_s32_headroom,
vect_complex_s16_headroom
参考性能 :
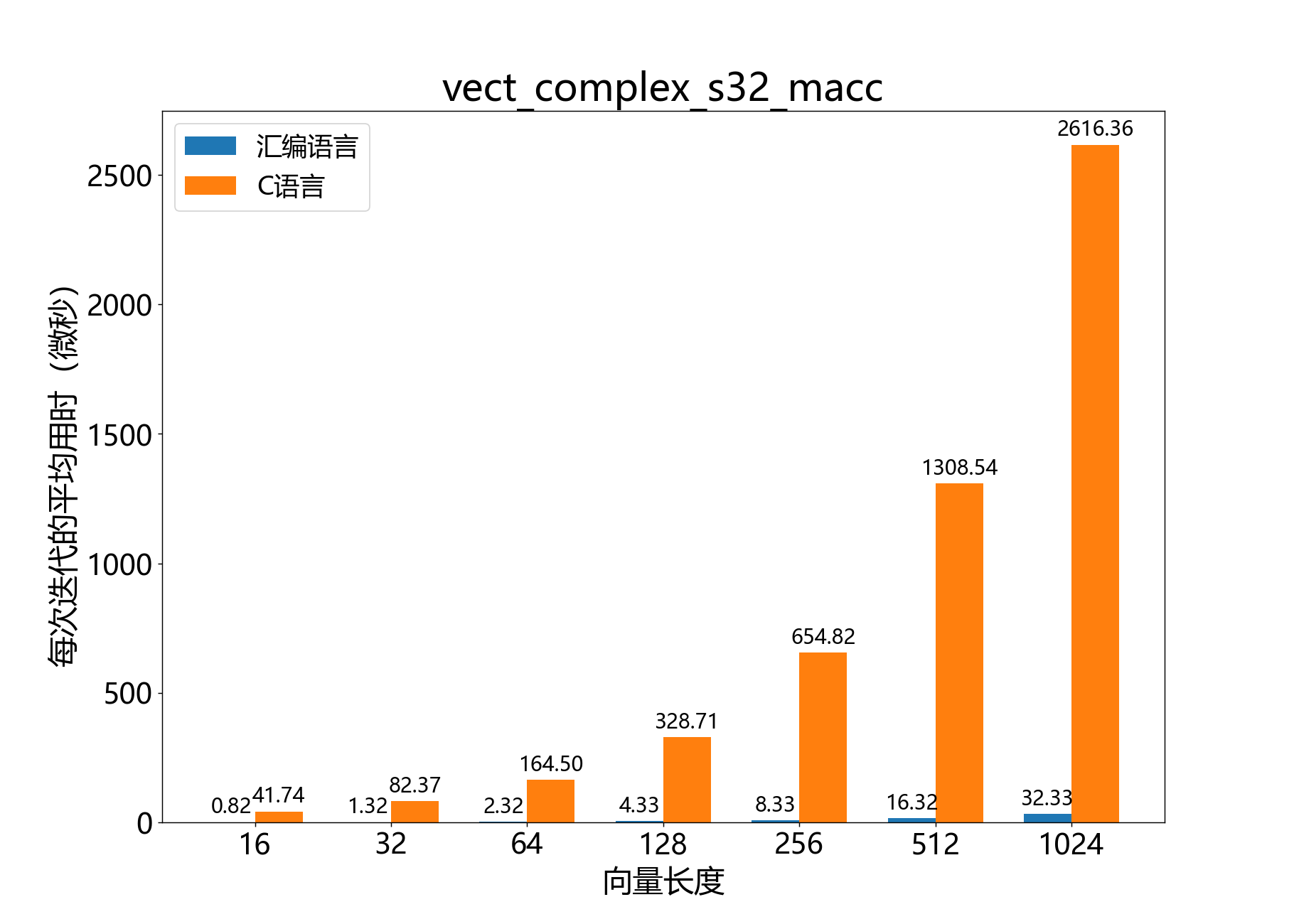
headroom_t vect_complex_s32_macc() 逐元素将一个复数32位向量与另一个复数32位向量相乘,并将结果添加到累加器中。
acc[]表示复数32位累加器尾数向量a ˉ \bar{a} a ˉ a k a_k a k acc[k]。
b[]和c[]表示复数32位输入尾数向量b ˉ \bar{b} b ˉ c ˉ \bar{c} c ˉ b k b_k b k b[k],每个c k c_k c k c[k]。
每个输入向量必须从字对齐的地址开始。
length是向量中的元素数量。
acc_shr,b_shr和c_shr是应用于输入元素a k a_k a k b k b_k b k c k c_k c k
操作定义为:
b ~ k ← s a t 32 ( b k ⋅ 2 − b _ s h r ) c ~ k ← s a t 32 ( c k ⋅ 2 − c _ s h r ) a ~ k ← s a t 32 ( a k ⋅ 2 − a c c _ s h r ) v k ← r o u n d ( s a t 32 ( ( R e { b ~ k } ⋅ R e { c ~ k } − I m { b ~ k } ⋅ I m { c ~ k } ) ⋅ 2 − 30 ) ) s k ← r o u n d ( s a t 32 ( ( I m { b ~ k } ⋅ R e { c ~ k } + R e { b ~ k } ⋅ I m { c ~ k } ) ⋅ 2 − 30 ) ) R e { a k } ← s a t 32 ( R e { a ~ k } + v k ) I m { a k } ← s a t 32 ( I m { a ~ k } + s k ) for k ∈ 0 . . . ( l e n g t h − 1 ) \begin{split}\begin{align*}
& \tilde{b}_k \leftarrow sat_{32}( b_k \cdot 2^{-b\_shr} ) \\
& \tilde{c}_k \leftarrow sat_{32}( c_k \cdot 2^{-c\_shr} ) \\
& \tilde{a}_k \leftarrow sat_{32}( a_k \cdot 2^{-acc\_shr} ) \\
& v_k \leftarrow round( sat_{32}( ( Re\{\tilde{b}_k\} \cdot Re\{\tilde{c}_k\} - Im\{\tilde{b}_k\} \cdot Im\{\tilde{c}_k\} ) \cdot 2^{-30}) ) \\
& s_k \leftarrow round( sat_{32}( ( Im\{\tilde{b}_k\} \cdot Re\{\tilde{c}_k\} + Re\{\tilde{b}_k\} \cdot Im\{\tilde{c}_k\} ) \cdot 2^{-30}) ) \\
& Re\{a_k\} \leftarrow sat_{32}( Re\{\tilde{a}_k\} + v_k ) \\
& Im\{a_k\} \leftarrow sat_{32}( Im\{\tilde{a}_k\} + s_k ) \\
& \qquad\text{ for }k\in 0\ ...\ (length-1) &&
\end{align*}\end{split} b ~ k ← s a t 32 ( b k ⋅ 2 − b _ s h r ) c ~ k ← s a t 32 ( c k ⋅ 2 − c _ s h r ) a ~ k ← s a t 32 ( a k ⋅ 2 − a cc _ s h r ) v k ← ro u n d ( s a t 32 (( R e { b ~ k } ⋅ R e { c ~ k } − I m { b ~ k } ⋅ I m { c ~ k }) ⋅ 2 − 30 )) s k ← ro u n d ( s a t 32 (( I m { b ~ k } ⋅ R e { c ~ k } + R e { b ~ k } ⋅ I m { c ~ k }) ⋅ 2 − 30 )) R e { a k } ← s a t 32 ( R e { a ~ k } + v k ) I m { a k } ← s a t 32 ( I m { a ~ k } + s k ) for k ∈ 0 ... ( l e n g t h − 1 ) 块浮点数:
如果输入b ˉ \bar{b} b ˉ c ˉ \bar{c} c ˉ b ˉ ⋅ 2 b _ e x p \bar{b} \cdot 2^{b\_exp} b ˉ ⋅ 2 b _ e x p c ˉ ⋅ 2 c _ e x p \bar{c} \cdot 2^{c\_exp} c ˉ ⋅ 2 c _ e x p a ˉ \bar{a} a ˉ a ˉ ⋅ 2 a _ e x p \bar{a} \cdot 2^{a\_exp} a ˉ ⋅ 2 a _ e x p a ˉ \bar{a} a ˉ 2 a _ e x p + a c c _ s h r 2^{a\_exp + acc\_shr} 2 a _ e x p + a cc _ s h r
为了使数学上的累加有意义,必须选择b c _ s a t bc\_sat b c _ s a t a _ e x p + a c c _ s h r = b _ e x p + c _ e x p + b _ s h r + c _ s h r a\_exp + acc\_shr = b\_exp + c\_exp + b\_shr + c\_shr a _ e x p + a cc _ s h r = b _ e x p + c _ e x p + b _ s h r + c _ s h r
可以使用函数vect_complex_s32_macc_prepare()根据输入指数a _ e x p a\_exp a _ e x p b _ e x p b\_exp b _ e x p c _ e x p c\_exp c _ e x p a _ h r a\_hr a _ h r b _ h r b\_hr b _ h r c _ h r c\_hr c _ h r a _ e x p a\_exp a _ e x p a c c _ s h r acc\_shr a cc _ s h r b _ s h r b\_shr b _ s h r c _ s h r c\_shr c _ s h r
参数:
complex_s32_t acc[] – [inout]a ˉ \bar{a} a ˉ
const complex_s32_t b[] – [in]b ˉ \bar{b} b ˉ
const complex_s32_t c[] – [in]c ˉ \bar{c} c ˉ
const unsigned length – [in]a ˉ \bar{a} a ˉ b ˉ \bar{b} b ˉ c ˉ \bar{c} c ˉ
const right_shift_t acc_shr – [in]
const right_shift_t b_shr – [in]b ˉ \bar{b} b ˉ
const right_shift_t c_shr – [in]c ˉ \bar{c} c ˉ
返回值:
异常:
如果acc,b或c不是字对齐的,则引发ET_LOAD_STORE异常(参见 笔记:向量对齐 )
另请参阅:
vect_complex_s32_macc_prepare
参考性能 :
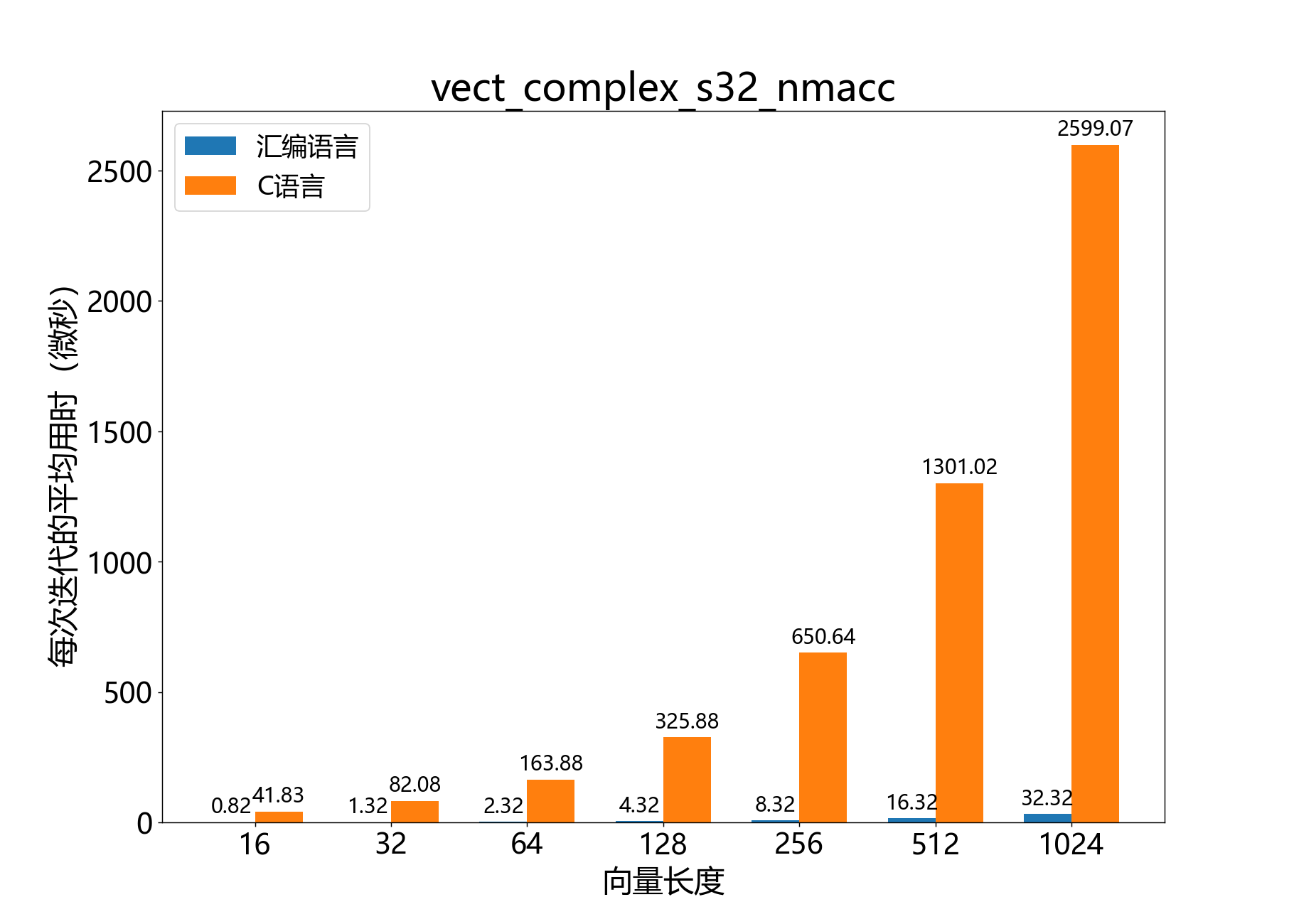
headroom_t vect_complex_s32_nmacc() 逐元素将一个复数32位向量与另一个向量相乘,并将结果从累加器中减去。
acc[]表示复数32位累加器的尾数向量 a ˉ \bar{a} a ˉ a k a_k a k acc[k]。
b[]和c[]表示复数32位输入尾数向量 b ˉ \bar{b} b ˉ c ˉ \bar{c} c ˉ b k b_k b k b[k],每个 c k c_k c k c[k]。
输入向量中的每个向量必须从字对齐的地址开始。
length是每个向量中的元素数量。
acc_shr、b_shr和c_shr是应用于输入元素 a k a_k a k b k b_k b k c k c_k c k
此函数执行的操作可以表示如下:
b ~ k ← s a t 32 ( b k ⋅ 2 − b _ s h r ) c ~ k ← s a t 32 ( c k ⋅ 2 − c _ s h r ) a ~ k ← s a t 32 ( a k ⋅ 2 − a c c _ s h r ) v k ← r o u n d ( s a t 32 ( ( R e { b ~ k } ⋅ R e { c ~ k } − I m { b ~ k } ⋅ I m { c ~ k } ) ⋅ 2 − 30 ) ) s k ← r o u n d ( s a t 32 ( ( I m { b ~ k } ⋅ R e { c ~ k } + R e { b ~ k } ⋅ I m { c ~ k } ) ⋅ 2 − 30 ) ) R e { a k } ← s a t 32 ( R e { a ~ k } − v k ) I m { a k } ← s a t 32 ( I m { a ~ k } − s k ) for k ∈ 0 . . . ( l e n g t h − 1 ) \begin{align*}
& \tilde{b}_k \leftarrow sat_{32}( b_k \cdot 2^{-b\_shr} ) \\
& \tilde{c}_k \leftarrow sat_{32}( c_k \cdot 2^{-c\_shr} ) \\
& \tilde{a}_k \leftarrow sat_{32}( a_k \cdot 2^{-acc\_shr} ) \\
& v_k \leftarrow round( sat_{32}( ( Re\{\tilde{b}_k\} \cdot Re\{\tilde{c}_k\} - Im\{\tilde{b}_k\} \cdot Im\{\tilde{c}_k\} ) \cdot 2^{-30}) ) \\
& s_k \leftarrow round( sat_{32}( ( Im\{\tilde{b}_k\} \cdot Re\{\tilde{c}_k\} + Re\{\tilde{b}_k\} \cdot Im\{\tilde{c}_k\} ) \cdot 2^{-30}) ) \\
& Re\{a_k\} \leftarrow sat_{32}( Re\{\tilde{a}_k\} - v_k ) \\
& Im\{a_k\} \leftarrow sat_{32}( Im\{\tilde{a}_k\} - s_k ) \\
& \qquad\text{ for }k\in 0\ ...\ (length-1)
\end{align*} b ~ k ← s a t 32 ( b k ⋅ 2 − b _ s h r ) c ~ k ← s a t 32 ( c k ⋅ 2 − c _ s h r ) a ~ k ← s a t 32 ( a k ⋅ 2 − a cc _ s h r ) v k ← ro u n d ( s a t 32 (( R e { b ~ k } ⋅ R e { c ~ k } − I m { b ~ k } ⋅ I m { c ~ k }) ⋅ 2 − 30 )) s k ← ro u n d ( s a t 32 (( I m { b ~ k } ⋅ R e { c ~ k } + R e { b ~ k } ⋅ I m { c ~ k }) ⋅ 2 − 30 )) R e { a k } ← s a t 32 ( R e { a ~ k } − v k ) I m { a k } ← s a t 32 ( I m { a ~ k } − s k ) for k ∈ 0 ... ( l e n g t h − 1 ) 块浮点数:
如果��输入 b ˉ \bar{b} b ˉ c ˉ \bar{c} c ˉ b ˉ ⋅ 2 b _ e x p \bar{b} \cdot 2^{b\_exp} b ˉ ⋅ 2 b _ e x p c ˉ ⋅ 2 c _ e x p \bar{c} \cdot 2^{c\_exp} c ˉ ⋅ 2 c _ e x p a ˉ \bar{a} a ˉ a ˉ ⋅ 2 a _ e x p \bar{a} \cdot 2^{a\_exp} a ˉ ⋅ 2 a _ e x p a ˉ \bar{a} a ˉ 2 a _ e x p + a c c _ s h r 2^{a\_exp + acc\_shr} 2 a _ e x p + a cc _ s h r
为了使累加在数学上有意义,必须选择 b c _ s a t bc\_sat b c _ s a t a _ e x p + a c c _ s h r = b _ e x p + c _ e x p + b _ s h r + c _ s h r a\_exp + acc\_shr = b\_exp + c\_exp + b\_shr + c\_shr a _ e x p + a cc _ s h r = b _ e x p + c _ e x p + b _ s h r + c _ s h r
函数vect_complex_s32_macc_prepare()可以根据输入指数 a _ e x p a\_exp a _ e x p b _ e x p b\_exp b _ e x p c _ e x p c\_exp c _ e x p a _ h r a\_hr a _ h r b _ h r b\_hr b _ h r c _ h r c\_hr c _ h r a _ e x p a\_exp a _ e x p a c c _ s h r acc\_shr a cc _ s h r b _ s h r b\_shr b _ s h r c _ s h r c\_shr c _ s h r
参数:
complex_s32_t acc[] – [inout]a ˉ \bar{a} a ˉ
const complex_s32_t b[] – [in]b ˉ \bar{b} b ˉ
const complex_s32_t c[] – [in]c ˉ \bar{c} c ˉ
const unsigned length – [in]a ˉ \bar{a} a ˉ b ˉ \bar{b} b ˉ c ˉ \bar{c} c ˉ
const right_shift_t acc_shr – [in]
const right_shift_t b_shr – [in]b ˉ \bar{b} b ˉ
const right_shift_t c_shr – [in]c ˉ \bar{c} c ˉ
返回值: 输出向量 a ˉ \bar{a} a ˉ
异常: 如果acc、b或c不是字对齐的,则引发ET_LOAD_STORE异常(参见 笔记:向量对齐 )
另请参阅: vect_complex_s32_nmacc_prepare
参考性能 :
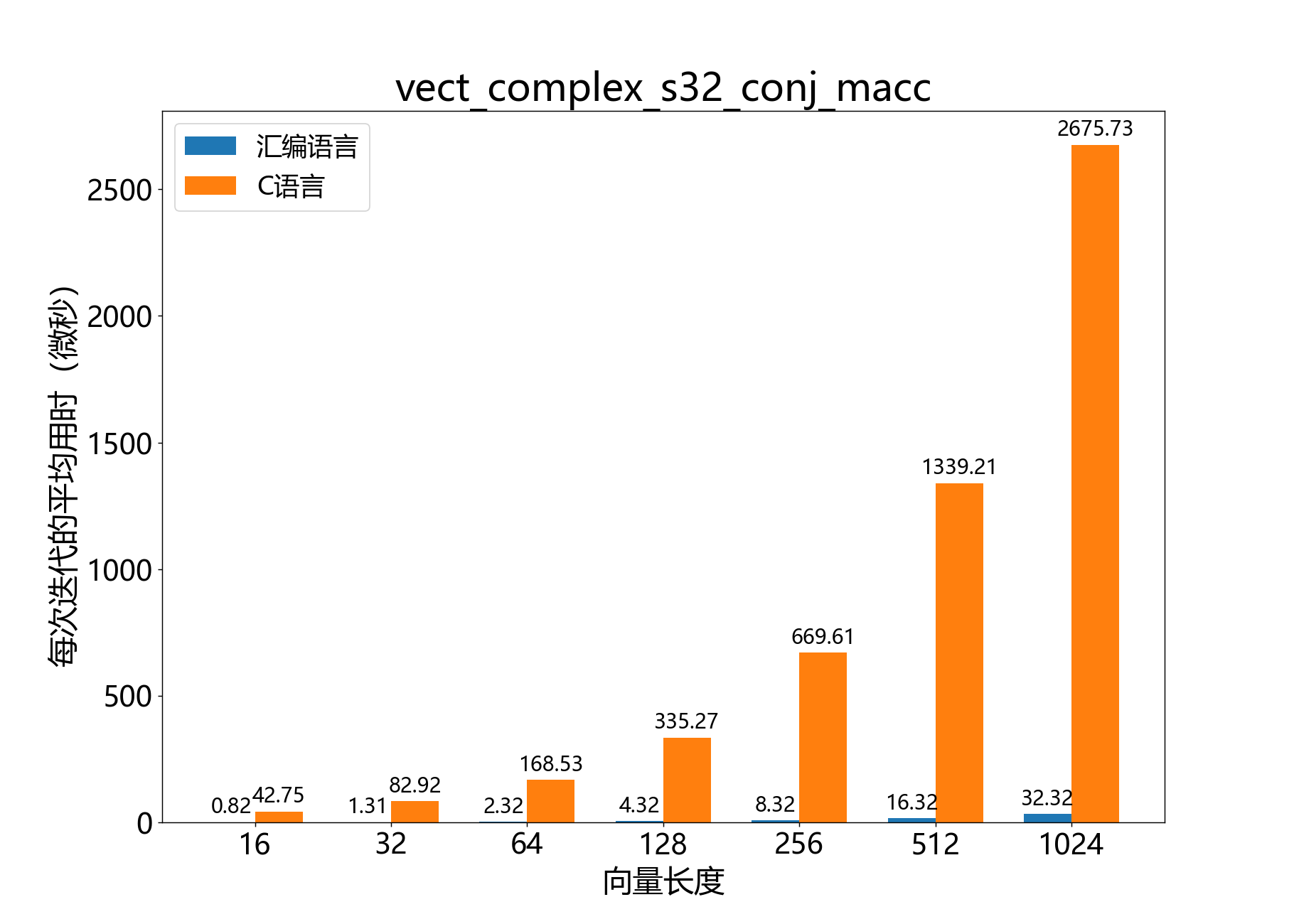
headroom_t vect_complex_s32_conj_macc() 逐元素将一个复数的32位向量与另一个复数的共轭相乘,并将结果累加到一个累加器中。
acc[] 表示复数32位累加器尾数向量 a ˉ \bar{a} a ˉ a k a_k a k acc[k]。
b[] 和 c[] 表示复数32位输入尾数向量 b ˉ \bar{b} b ˉ c ˉ \bar{c} c ˉ b k b_k b k b[k],每个 c k c_k c k c[k]。
每个输入向量必须从字对齐的地址开始。
length 是每个向量中的元素数量。
acc_shr、b_shr 和 c_shr 是应用于输入元素 a k a_k a k b k b_k b k c k c_k c k
操作:
b ~ k ← s a t 32 ( b k ⋅ 2 − b _ s h r ) c ~ k ← s a t 32 ( c k ⋅ 2 − c _ s h r ) a ~ k ← s a t 32 ( a k ⋅ 2 − a c c _ s h r ) v k ← r o u n d ( s a t 32 ( ( R e { b ~ k } ⋅ R e { c ~ k } + I m { b ~ k } ⋅ I m { c ~ k } ) ⋅ 2 − 30 ) ) s k ← r o u n d ( s a t 32 ( ( I m { b ~ k } ⋅ R e { c ~ k } − R e { b ~ k } ⋅ I m { c ~ k } ) ⋅ 2 − 30 ) ) R e { a k } ← s a t 32 ( R e { a ~ k } + v k ) I m { a k } ← s a t 32 ( I m { a ~ k } + s k ) 其中 k ∈ 0 . . . ( l e n g t h − 1 ) \begin{align*}
& \tilde{b}_k \leftarrow sat_{32}( b_k \cdot 2^{-b\_shr} ) \\
& \tilde{c}_k \leftarrow sat_{32}( c_k \cdot 2^{-c\_shr} ) \\
& \tilde{a}_k \leftarrow sat_{32}( a_k \cdot 2^{-acc\_shr} ) \\
& v_k \leftarrow round( sat_{32}( ( Re\{\tilde{b}_k\} \cdot Re\{\tilde{c}_k\} + Im\{\tilde{b}_k\} \cdot Im\{\tilde{c}_k\} ) \cdot 2^{-30}) ) \\
& s_k \leftarrow round( sat_{32}( ( Im\{\tilde{b}_k\} \cdot Re\{\tilde{c}_k\} - Re\{\tilde{b}_k\} \cdot Im\{\tilde{c}_k\} ) \cdot 2^{-30}) ) \\
& Re\{a_k\} \leftarrow sat_{32}( Re\{\tilde{a}_k\} + v_k ) \\
& Im\{a_k\} \leftarrow sat_{32}( Im\{\tilde{a}_k\} + s_k ) \\
& \qquad\text{其中} \quad k\in 0\ ...\ (length-1)
\end{align*} b ~ k ← s a t 32 ( b k ⋅ 2 − b _ s h r ) c ~ k ← s a t 32 ( c k ⋅ 2 − c _ s h r ) a ~ k ← s a t 32 ( a k ⋅ 2 − a cc _ s h r ) v k ← ro u n d ( s a t 32 (( R e { b ~ k } ⋅ R e { c ~ k } + I m { b ~ k } ⋅ I m { c ~ k }) ⋅ 2 − 30 )) s k ← ro u n d ( s a t 32 (( I m { b ~ k } ⋅ R e { c ~ k } − R e { b ~ k } ⋅ I m { c ~ k }) ⋅ 2 − 30 )) R e { a k } ← s a t 32 ( R e { a ~ k } + v k ) I m { a k } ← s a t 32 ( I m { a ~ k } + s k ) 其中 k ∈ 0 ... ( l e n g t h − 1 ) 块浮点数:
如果输入 b ˉ \bar{b} b ˉ c ˉ \bar{c} c ˉ b ˉ ⋅ 2 b _ e x p \bar{b} \cdot 2^{b\_exp} b ˉ ⋅ 2 b _ e x p c ˉ ⋅ 2 c _ e x p \bar{c} \cdot 2^{c\_exp} c ˉ ⋅ 2 c _ e x p a ˉ \bar{a} a ˉ a ˉ ⋅ 2 a _ e x p \bar{a} \cdot 2^{a\_exp} a ˉ ⋅ 2 a _ e x p a ˉ \bar{a} a ˉ 2 a _ e x p + a c c _ s h r 2^{a\_exp + acc\_shr} 2 a _ e x p + a cc _ s h r
为了使累加在数学上有意义,必须选择 b c _ s a t bc\_sat b c _ s a t a _ e x p + a c c _ s h r = b _ e x p + c _ e x p + b _ s h r + c _ s h r a\_exp + acc\_shr = b\_exp + c\_exp + b\_shr + c\_shr a _ e x p + a cc _ s h r = b _ e x p + c _ e x p + b _ s h r + c _ s h r
可以使用函数 vect_complex_s32_conj_macc_prepare() 基于输入的指数 a _ e x p a\_exp a _ e x p b _ e x p b\_exp b _ e x p c _ e x p c\_exp c _ e x p a _ h r a\_hr a _ h r b _ h r b\_hr b _ h r c _ h r c\_hr c _ h r a _ e x p a\_exp a _ e x p a c c _ s h r acc\_shr a cc _ s h r b _ s h r b\_shr b _ s h r c _ s h r c\_shr c _ s h r
参数:
complex_s32_t acc[] – [inout]a ˉ \bar{a} a ˉ const complex_s32_t b[] – [in]b ˉ \bar{b} b ˉ const complex_s32_t c[] – [in]c ˉ \bar{c} c ˉ const unsigned length – [in]a ˉ \bar{a} a ˉ b ˉ \bar{b} b ˉ c ˉ \bar{c} c ˉ const right_shift_t acc_shr – [in]const right_shift_t b_shr – [in]b ˉ \bar{b} b ˉ const right_shift_t c_shr – [in]c ˉ \bar{c} c ˉ
返回值: 输出向量 a ˉ \bar{a} a ˉ
异常: 如果 acc、b 或 c 不是字对齐的,则引发 ET_LOAD_STORE 异常(参见 笔记:向量对齐 )。
参见: vect_complex_s32_conj_macc_prepare
参考性能 :
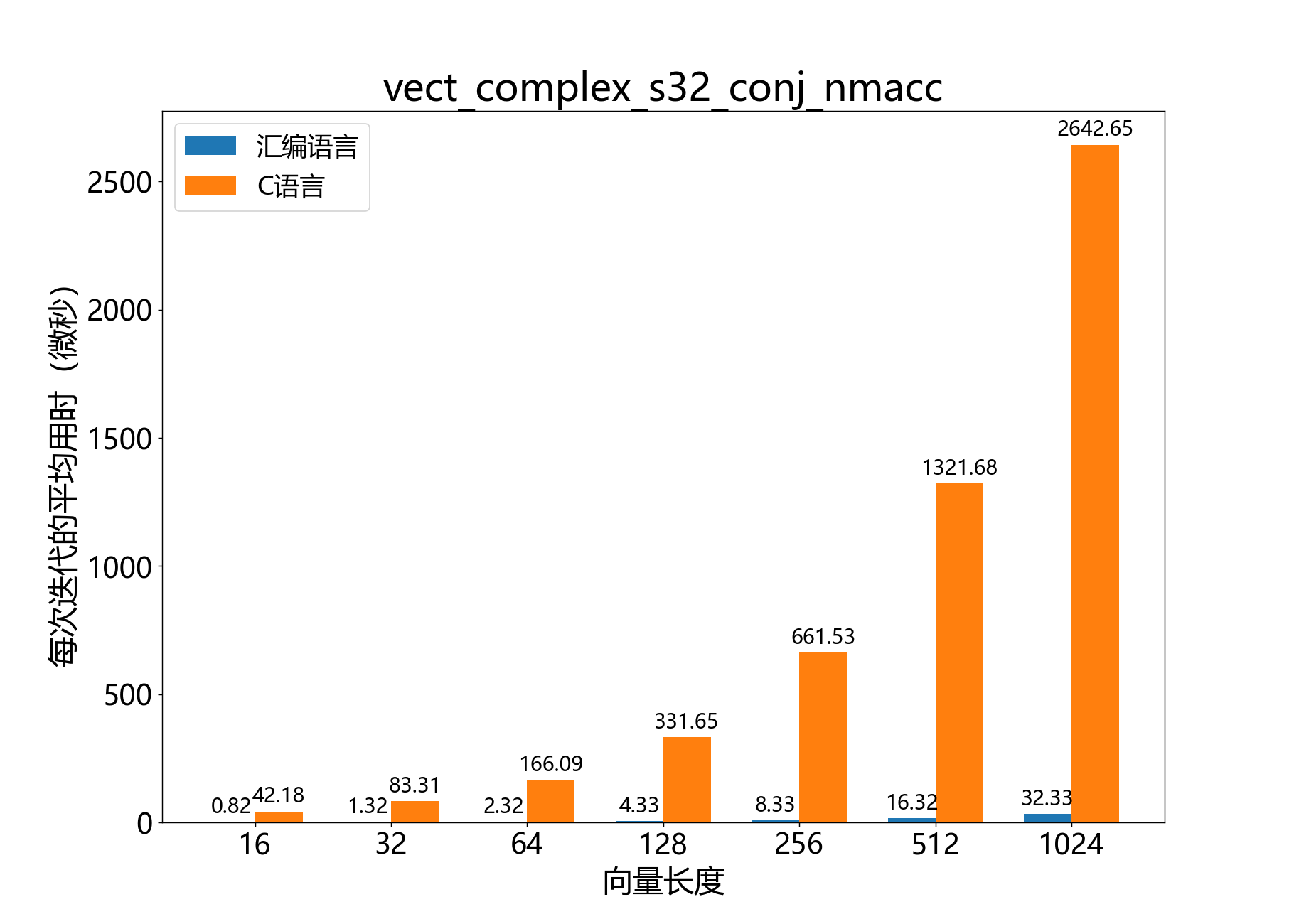
headroom_t vect_complex_s32_conj_nmacc() 逐元素将一个复数的32位向量与另一个复数的共轭相乘,并从累加器中减去结果。
acc[] 表示复数32位累加器尾数向量 a ˉ \bar{a} a ˉ a k a_k a k acc[k]。
b[] 和 c[] 表示复数32位输入尾数向量 b ˉ \bar{b} b ˉ c ˉ \bar{c} c ˉ b k b_k b k b[k],每个 c k c_k c k c[k]。
每个输入向量必须从字对齐的地址开始。
length 是每个向量中的元素数量。
acc_shr、b_shr 和 c_shr 是应用于输入元素 a k a_k a k b k b_k b k c k c_k c k
操作:
b ~ k ← s a t 32 ( b k ⋅ 2 − b _ s h r ) c ~ k ← s a t 32 ( c k ⋅ 2 − c _ s h r ) a ~ k ← s a t 32 ( a k �⋅ 2 − a c c _ s h r ) v k ← r o u n d ( s a t 32 ( ( R e { b ~ k } ⋅ R e { c ~ k } + I m { b ~ k } ⋅ I m { c ~ k } ) ⋅ 2 − 30 ) ) s k ← r o u n d ( s a t 32 ( ( I m { b ~ k } ⋅ R e { c ~ k } − R e { b ~ k } ⋅ I m { c ~ k } ) ⋅ 2 − 30 ) ) R e { a k } ← s a t 32 ( R e { a ~ k } − v k ) I m { a k } ← s a t 32 ( I m { a ~ k } − s k ) 其中 k ∈ 0 . . . ( l e n g t h − 1 ) \begin{align*}
& \tilde{b}_k \leftarrow sat_{32}( b_k \cdot 2^{-b\_shr} ) \\
& \tilde{c}_k \leftarrow sat_{32}( c_k \cdot 2^{-c\_shr} ) \\
& \tilde{a}_k \leftarrow sat_{32}( a_k \cdot 2^{-acc\_shr} ) \\
& v_k \leftarrow round( sat_{32}( ( Re\{\tilde{b}_k\} \cdot Re\{\tilde{c}_k\} + Im\{\tilde{b}_k\} \cdot Im\{\tilde{c}_k\} ) \cdot 2^{-30}) ) \\
& s_k \leftarrow round( sat_{32}( ( Im\{\tilde{b}_k\} \cdot Re\{\tilde{c}_k\} - Re\{\tilde{b}_k\} \cdot Im\{\tilde{c}_k\} ) \cdot 2^{-30}) ) \\
& Re\{a_k\} \leftarrow sat_{32}( Re\{\tilde{a}_k\} - v_k ) \\
& Im\{a_k\} \leftarrow sat_{32}( Im\{\tilde{a}_k\} - s_k ) \\
& \qquad\text{其中} \quad k\in 0\ ...\ (length-1)
\end{align*} b ~ k ← s a t 32 ( b k ⋅ 2 − b _ s h r ) c ~ k ← s a t 32 ( c k ⋅ 2 − c _ s h r ) a ~ k ← s a t 32 ( a k ⋅ 2 − a cc _ s h r ) v k ← ro u n d ( s a t 32 (( R e { b ~ k } ⋅ R e { c ~ k } + I m { b ~ k } ⋅ I m { c ~ k }) ⋅ 2 − 30 )) s k ← ro u n d ( s a t 32 (( I m { b ~ k } ⋅ R e { c ~ k } − R e { b ~ k } ⋅ I m { c ~ k }) ⋅ 2 − 30 )) R e { a k } ← s a t 32 ( R e { a ~ k } − v k ) I m { a k } ← s a t 32 ( I m { a ~ k } − s k ) 其中 k ∈ 0 ... ( l e n g t h − 1 ) 块浮点数:
如果输入 b ˉ \bar{b} b ˉ c ˉ \bar{c} c ˉ b ˉ ⋅ 2 b _ e x p \bar{b} \cdot 2^{b\_exp} b ˉ ⋅ 2 b _ e x p c ˉ ⋅ 2 c _ e x p \bar{c} \cdot 2^{c\_exp} c ˉ ⋅ 2 c _ e x p a ˉ \bar{a} a ˉ a ˉ ⋅ 2 a _ e x p \bar{a} \cdot 2^{a\_exp} a ˉ ⋅ 2 a _ e x p a ˉ \bar{a} a ˉ 2 a _ e x p + a c c _ s h r 2^{a\_exp + acc\_shr} 2 a _ e x p + a cc _ s h r
为了使累加在数学上有意义,必须选择 b c _ s a t bc\_sat b c _ s a t a _ e x p + a c c _ s h r = b _ e x p + c _ e x p + b _ s h r + c _ s h r a\_exp + acc\_shr = b\_exp + c\_exp + b\_shr + c\_shr a _ e x p + a cc _ s h r = b _ e x p + c _ e x p + b _ s h r + c _ s h r
可以使用函数 vect_complex_s32_conj_nmacc_prepare() 基于输入的指数 a _ e x p a\_exp a _ e x p b _ e x p b\_exp b _ e x p c _ e x p c\_exp c _ e x p a _ h r a\_hr a _ h r b _ h r b\_hr b _ h r c _ h r c\_hr c _ h r a _ e x p a\_exp a _ e x p a c c _ s h r acc\_shr a cc _ s h r b _ s h r b\_shr b _ s h r c _ s h r c\_shr c _ s h r
参数:
complex_s32_t acc[] – [inout]a ˉ \bar{a} a ˉ const complex_s32_t b[] – [in]b ˉ \bar{b} b ˉ const complex_s32_t c[] – [in]c ˉ \bar{c} c ˉ const unsigned length – [in]a ˉ \bar{a} a ˉ b ˉ \bar{b} b ˉ c ˉ \bar{c} c ˉ const right_shift_t acc_shr – [in]const right_shift_t b_shr – [in]b ˉ \bar{b} b ˉ const right_shift_t c_shr – [in]c ˉ \bar{c} c ˉ
返回值: 输出向�量 a ˉ \bar{a} a ˉ
异常: 如果 acc、b 或 c 不是字对齐的,则引发 ET_LOAD_STORE 异常(参见 笔记:向量对齐 )。
参见: vect_complex_s32_conj_nmacc_prepare
参考性能 :
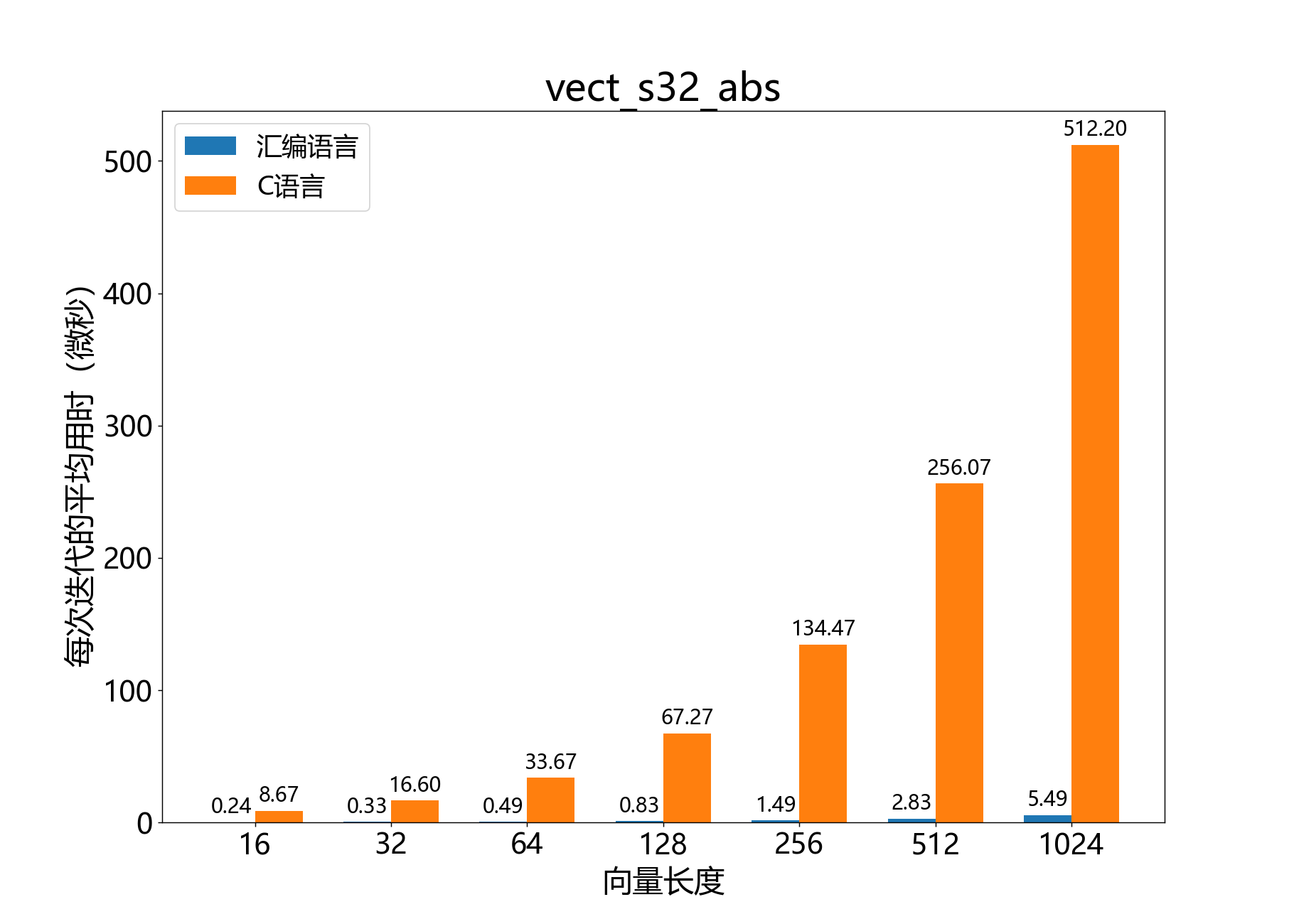
headroom_t vect_s32_abs() 计算32位向量的逐元素绝对值。
a[] 和 b[] 分别表示32位向量 a ˉ \bar{a} a ˉ b ˉ \bar{b} b ˉ b[] 上安全地原地执行。length 是向量中的元素数量。
操作:
a k ← s a t 32 ( ∣ b k ∣ ) 其中 k ∈ 0 . . . ( l e n g t h − 1 ) \begin{align*}
& a_k \leftarrow sat_{32}(\left| b_k \right|) \\
& \qquad\text{其中 } k \in 0\ ...\ (length-1)
\end{align*} a k ← s a t 32 ( ∣ b k ∣ ) 其中 k ∈ 0 ... ( l e n g t h − 1 ) 块浮点数:
如果 b ˉ \bar{b} b ˉ b ˉ ⋅ 2 b _ e x p \bar{b} \cdot 2^{b\_exp} b ˉ ⋅ 2 b _ e x p a ˉ \bar{a} a ˉ a ˉ ⋅ 2 a _ e x p \bar{a} \cdot 2^{a\_exp} a ˉ ⋅ 2 a _ e x p a _ e x p = b _ e x p a\_exp = b\_exp a _ e x p = b _ e x p
参数:
int32_t a[] – [out]a ˉ \bar{a} a ˉ const int32_t b[] – [in]b ˉ \bar{b} b ˉ const unsigned length – [in]a ˉ \bar{a} a ˉ b ˉ \bar{b} b ˉ
返回值:
headroom_ta ˉ \bar{a} a ˉ
异常:
ET_LOAD_STOREa 或 b 不是字对齐的(参见 笔记:向量对齐 )
相关:
参考性能 :
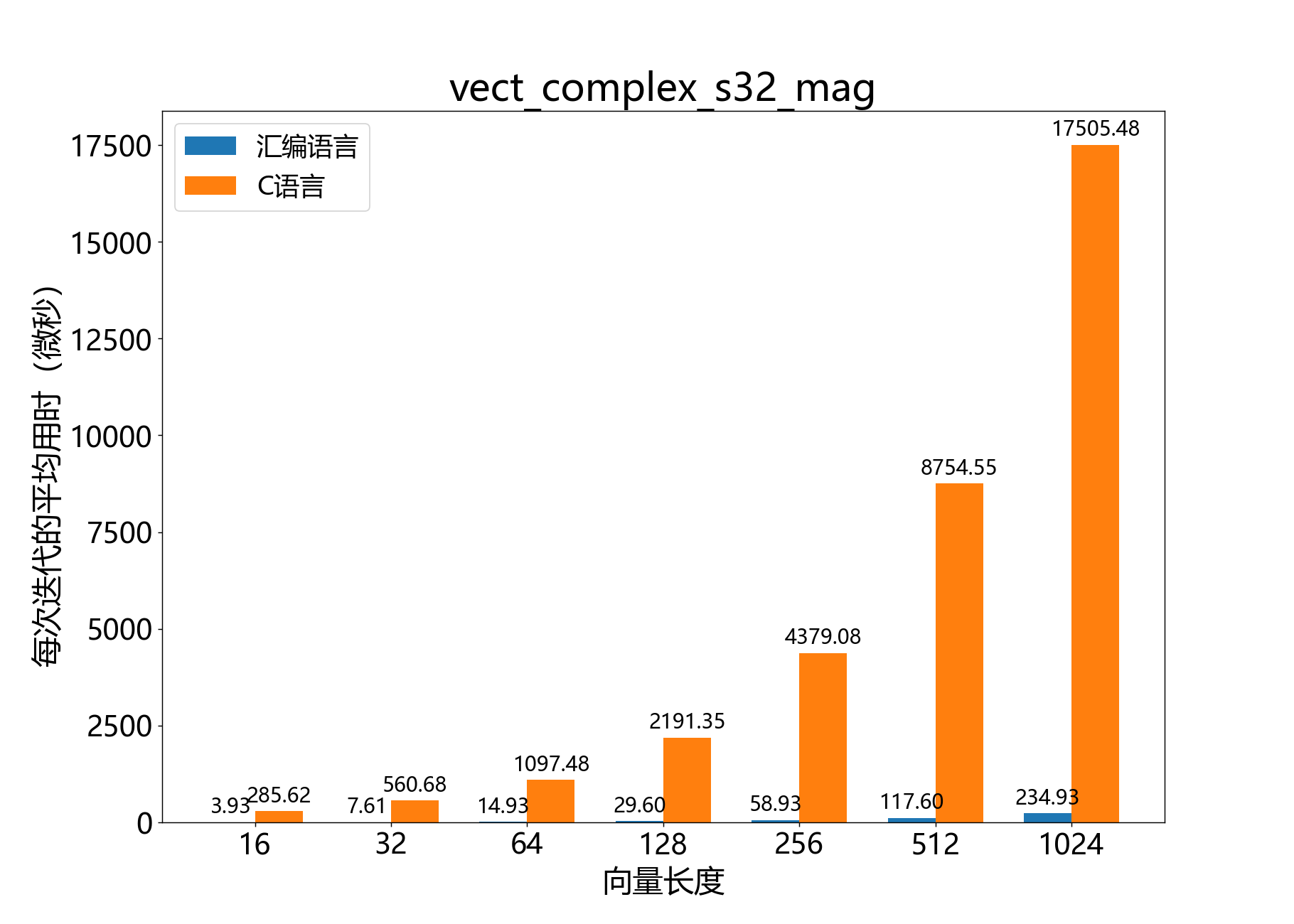
headroom_t vect_complex_s32_mag() 计算复数32位向量的每个元素的幅值。
a[] 表示实部32位输出尾数向量 a ˉ \bar{a} a ˉ b[] 表示复数32位输入尾数向量 b ˉ \bar{b} b ˉ a[] 和 b[] 必须从字对齐的地址开始。length 是向量中的元素数量。b_shr 是应用于 b ˉ \bar{b} b ˉ rot_table 必须指向一个预先计算的复数向量表,用于计算幅值。table_rows 是表中的行数。
该库附带了所需旋转表的默认版本。可以使用以下符号在用户代码中引用它:
const extern unsigned rot_table32_rows ; const extern complex_s32_t rot_table32 [ 30 ] [ 4 ] ; 通过生成较小版本的表格,可以实现更快的�计算(精度降低)。提供了一个Python脚本来生成这个表格。
此函数执行的操作如下:
v k ← b k ⋅ 2 − b _ s h r a k ← ( R e v k ) 2 + ( I m v k ) 2 其中 k ∈ 0 . . . ( l e n g t h − 1 ) v_k \leftarrow b_k \cdot 2^{-b\_shr} \\
a_k \leftarrow \sqrt { {\left( Re\\{v_k\\} \right)}^2 + {\left( Im\\{v_k\\} \right)}^2 } \\
\qquad\text{其中 } k \in 0\ ...\ (length-1) v k ← b k ⋅ 2 − b _ s h r a k ← ( R e v k ) 2 + ( I m v k ) 2 其中 k ∈ 0 ... ( l e n g t h − 1 ) 参数:
int32_t a[] – [out]a ˉ \bar{a} a ˉ const complex_s32_t b[] – [in]b ˉ \bar{b} b ˉ const unsigned length – [in]a ˉ \bar{a} a ˉ b ˉ \bar{b} b ˉ const right_shift_t b_shr – [in]b ˉ \bar{b} b ˉ const complex_s32_t* rot_table – [in]const unsigned table_rows – [in]rot_table 中的行数
返回值:
headroom_ta ˉ \bar{a} a ˉ
异常:
ET_LOAD_STOREa 或 b 不是字对齐的
相关:
vect_complex_s32_mag_prepare
参考性能 :
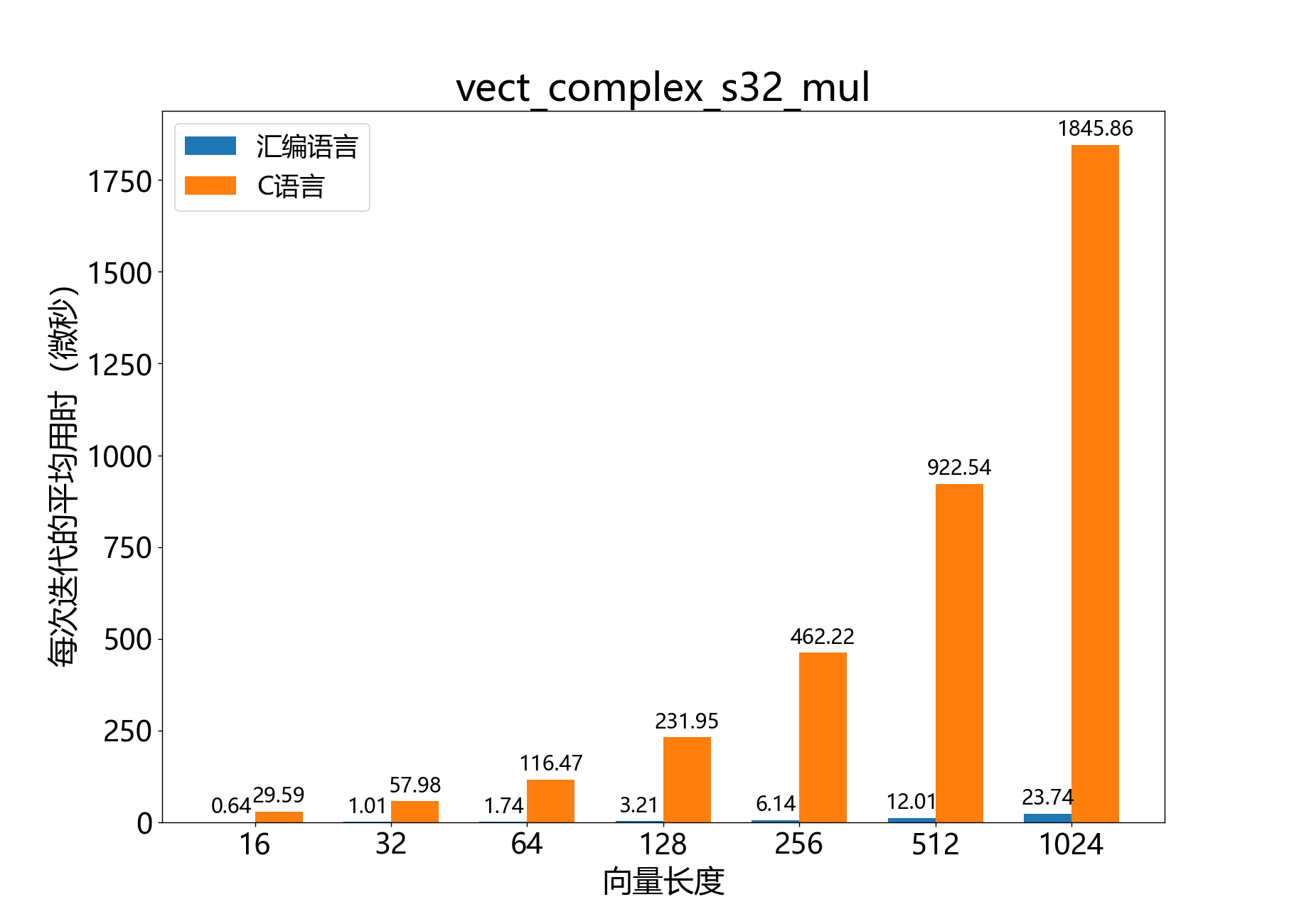
headroom_t vect_complex_s32_mul() 逐元素将一个复数32位向量与另一个复数32位向量相乘。
a[]、b[] 和 c[] 分别表示32位尾数向量 a ˉ \bar{a} a ˉ b ˉ \bar{b} b ˉ c ˉ \bar{c} c ˉ b[] 或 c[] 上安全地原地执行。length 是向量中的元素数量。b_shr 和 c_shr 是应用于 b ˉ \bar{b} b ˉ c ˉ \bar{c} c ˉ
操作:
b k ′ ← s a t 32 ( ⌊ b k ⋅ 2 − b _ s h r ⌋ ) c k ′ ← s a t 32 ( ⌊ c k ⋅ 2 − c _ s h r ⌋ ) R e { a k } ← ( R e { b k ′ } ⋅ R e { c k ′ } − I m { b k ′ } ⋅ I m { c k ′ } ) ⋅ 2 − 30 I m { a k } ← ( I m { b k ′ } ⋅ R e { c k ′ } + R e { b k ′ } ⋅ I m { c k ′ } ) ⋅ 2 − 30 其中 k ∈ 0 . . . ( l e n g t h − 1 ) \begin{align*}
& b_k' \leftarrow sat_{32}(\lfloor b_k \cdot 2^{-b\_shr} \rfloor) \\
& c_k' \leftarrow sat_{32}(\lfloor c_k \cdot 2^{-c\_shr} \rfloor) \\
& Re\{a_k\} \leftarrow \left( Re\{b_k'\} \cdot Re\{c_k'\} - Im\{b_k'\} \cdot Im\{c_k'\} \right) \cdot 2^{-30} \\
& Im\{a_k\} \leftarrow \left( Im\{b_k'\} \cdot Re\{c_k'\} + Re\{b_k'\} \cdot Im\{c_k'\} \right) \cdot 2^{-30} \\
& \qquad\text{其中 } k \in 0\ ...\ (length-1)
\end{align*} b k ′ ← s a t 32 (⌊ b k ⋅ 2 − b _ s h r ⌋) c k ′ ← s a t 32 (⌊ c k ⋅ 2 − c _ s h r ⌋) R e { a k } ← ( R e { b k ′ } ⋅ R e { c k ′ } − I m { b k ′ } ⋅ I m { c k ′ } ) ⋅ 2 − 30 I m { a k } ← ( I m { b k ′ } ⋅ R e { c k ′ } + R e { b k ′ } ⋅ I m { c k ′ } ) ⋅ 2 − 30 其中 k ∈ 0 ... ( l e n g t h − 1 ) 块浮点数:
如果 b ˉ \bar{b} b ˉ b ˉ ⋅ 2 b _ e x p \bar{b} \cdot 2^{b\_exp} b ˉ ⋅ 2 b _ e x p c c c c ⋅ 2 c _ e x p c \cdot 2^{c\_exp} c ⋅ 2 c _ e x p a ˉ \bar{a} a ˉ a ˉ ⋅ 2 a _ e x p \bar{a} \cdot 2^{a\_exp} a ˉ ⋅ 2 a _ e x p a _ e x p = b _ e x p + c _ e x p + b _ s h r + c _ s h r a\_exp = b\_exp + c\_exp + b\_shr + c\_shr a _ e x p = b _ e x p + c _ e x p + b _ s h r + c _ s h r
可以使用函数 vect_complex_s32_mul_prepare() 根据输入指数 b _ e x p b\_exp b _ e x p c _ e x p c\_exp c _ e x p b _ h r b\_hr b _ h r c _ h r c\_hr c _ h r a _ e x p a\_exp a _ e x p b _ s h r b\_shr b _ s h r c _ s h r c\_shr c _ s h r
参数:
complex_s32_t a[] – [out]a ˉ \bar{a} a ˉ const complex_s32_t b[] – [in]b ˉ \bar{b} b ˉ const complex_s32_t c[] – [in]c ˉ \bar{c} c ˉ const unsigned length – [in]a ˉ \bar{a} a ˉ b ˉ \bar{b} b ˉ c ˉ \bar{c} c ˉ const right_shift_t b_shr – [in]b ˉ \bar{b} b ˉ const right_shift_t c_shr – [in]c ˉ \bar{c} c ˉ
返回值:
headroom_ta ˉ \bar{a} a ˉ
异常:
ET_LOAD_STOREa、b 或 c 不是字对齐的
相关:
vect_complex_s32_mul_prepare
参考性能 :
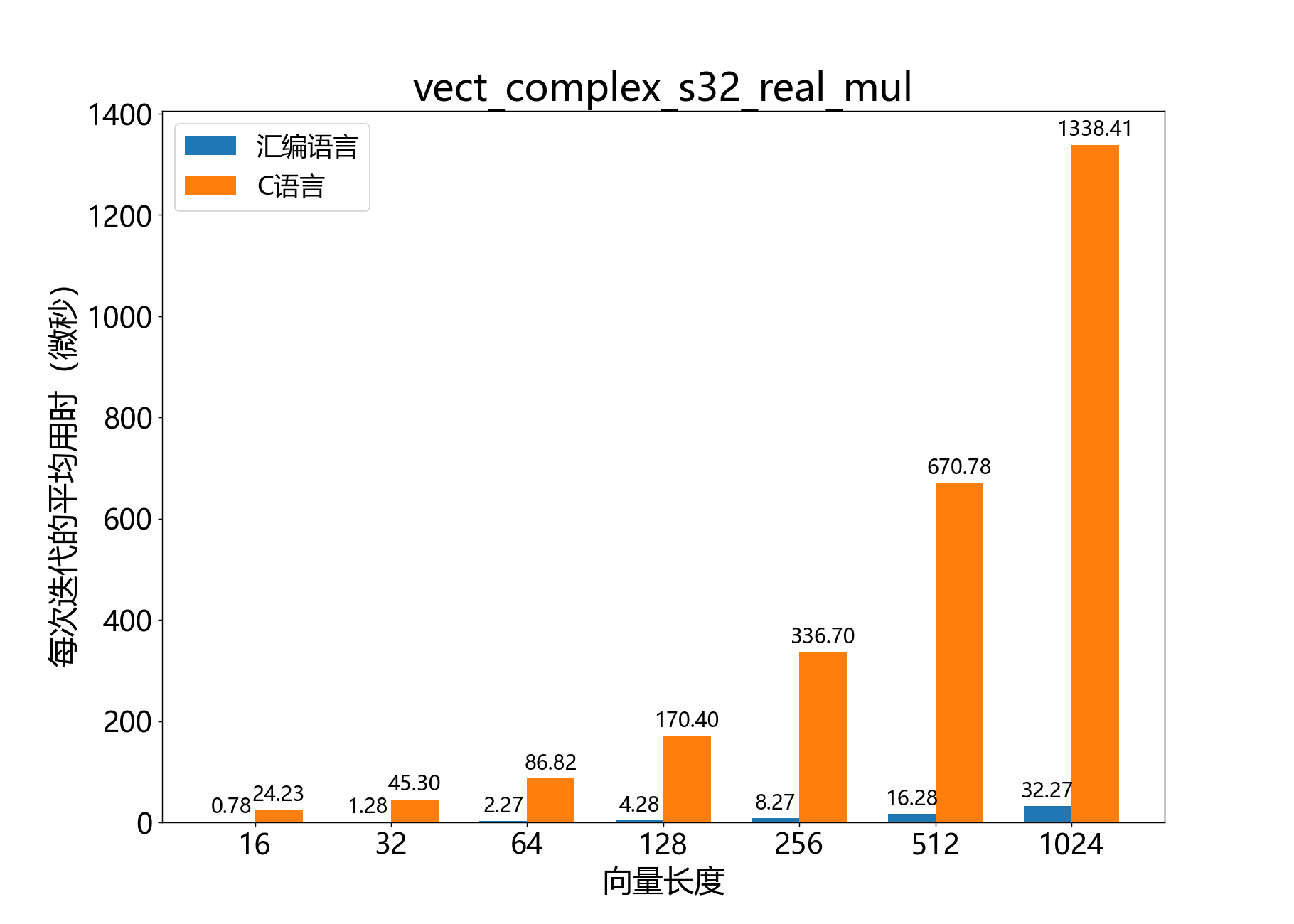
headroom_t vect_complex_s32_real_mul() 逐元素将复数32位向量与实数32位向量相乘。
a[]和b[]分别表示复数32位尾数向量 a ˉ \bar{a} a ˉ b ˉ \bar{b} b ˉ c[]表示实数32位尾数向量 c ˉ \bar{c} c ˉ
a[]、b[]和c[]必须从字对齐的地址开始。这个操作可以在b[]上安全地原地执行。
length是每个向量中的元素数量。
b_shr和c_shr是应用于 b ˉ \bar{b} b ˉ c ˉ \bar{c} c ˉ
操作:
b k ′ ← s a t 32 ( ⌊ b k ⋅ 2 − b _ s h r ⌋ ) c k ′ ← s a t 32 ( ⌊ c k ⋅ 2 − c _ s h r ⌋ ) R e { a k } ← ( R e { b k ′ } ⋅ c k ′ ) ⋅ 2 − 30 I m { a k } ← ( I m { b k ′ } ⋅ c k ′ ) ⋅ 2 − 30 其中 k ∈ 0 . . . ( l e n g t h − 1 ) \begin{split}\begin{align*} & b_k' \leftarrow sat_{32}(\lfloor b_k \cdot 2^{-b\_shr} \rfloor) \\ & c_k' \leftarrow sat_{32}(\lfloor c_k \cdot 2^{-c\_shr} \rfloor) \\ & Re\{a_k\} \leftarrow \left( Re\{b_k'\} \cdot c_k' \right) \cdot 2^{-30} \\ & Im\{a_k\} \leftarrow \left( Im\{b_k'\} \cdot c_k' \right) \cdot 2^{-30} \\ & \qquad\text{ 其中 }k\in 0\ ...\ (length-1) && \end{align*}\end{split} b k ′ ← s a t 32 (⌊ b k ⋅ 2 − b _ s h r ⌋) c k ′ ← s a t 32 (⌊ c k ⋅ 2 − c _ s h r ⌋) R e { a k } ← ( R e { b k ′ } ⋅ c k ′ ) ⋅ 2 − 30 I m { a k } ← ( I m { b k ′ } ⋅ c k ′ ) ⋅ 2 − 30 其中 k ∈ 0 ... ( l e n g t h − 1 ) 块浮点数:
如果 b ˉ \bar{b} b ˉ b ˉ ⋅ 2 b _ e x p \bar{b} \cdot 2^{b\_exp} b ˉ ⋅ 2 b _ e x p c ˉ \bar{c} c ˉ c ⋅ 2 c _ e x p c \cdot 2^{c\_exp} c ⋅ 2 c _ e x p a ˉ \bar{a} a ˉ a ˉ ⋅ 2 a _ e x p \bar{a} \cdot 2^{a\_exp} a ˉ ⋅ 2 a _ e x p a _ e x p = b _ e x p + c _ e x p + b _ s h r + c _ s h r a\_exp = b\_exp + c\_exp + b\_shr + c\_shr a _ e x p = b _ e x p + c _ e x p + b _ s h r + c _ s h r
函数vect_complex_s32_real_mul_prepare()可以根据输入指数 b _ e x p b\_exp b _ e x p c _ e x p c\_exp c _ e x p b _ h r b\_hr b _ h r c _ h r c\_hr c _ h r a _ e x p a\_exp a _ e x p b _ s h r b\_shr b _ s h r c _ s h r c\_shr c _ s h r
参数:
complex_s32_t a[] – [out]a ˉ \bar{a} a ˉ const complex_s32_t b[] – [in]b ˉ \bar{b} b ˉ const int32_t c[] – [in]c ˉ \bar{c} c ˉ const unsigned length – [in]a ˉ \bar{a} a ˉ b ˉ \bar{b} b ˉ c ˉ \bar{c} c ˉ const right_shift_t b_shr – [in]b ˉ \bar{b} b ˉ const right_shift_t c_shr – [in]c ˉ \bar{c} c ˉ
返回值:
异常:
如果a、b或c不是字对齐的,则引发ET_LOAD_STORE异常(参见笔记:向量对齐 )
参考性能 :
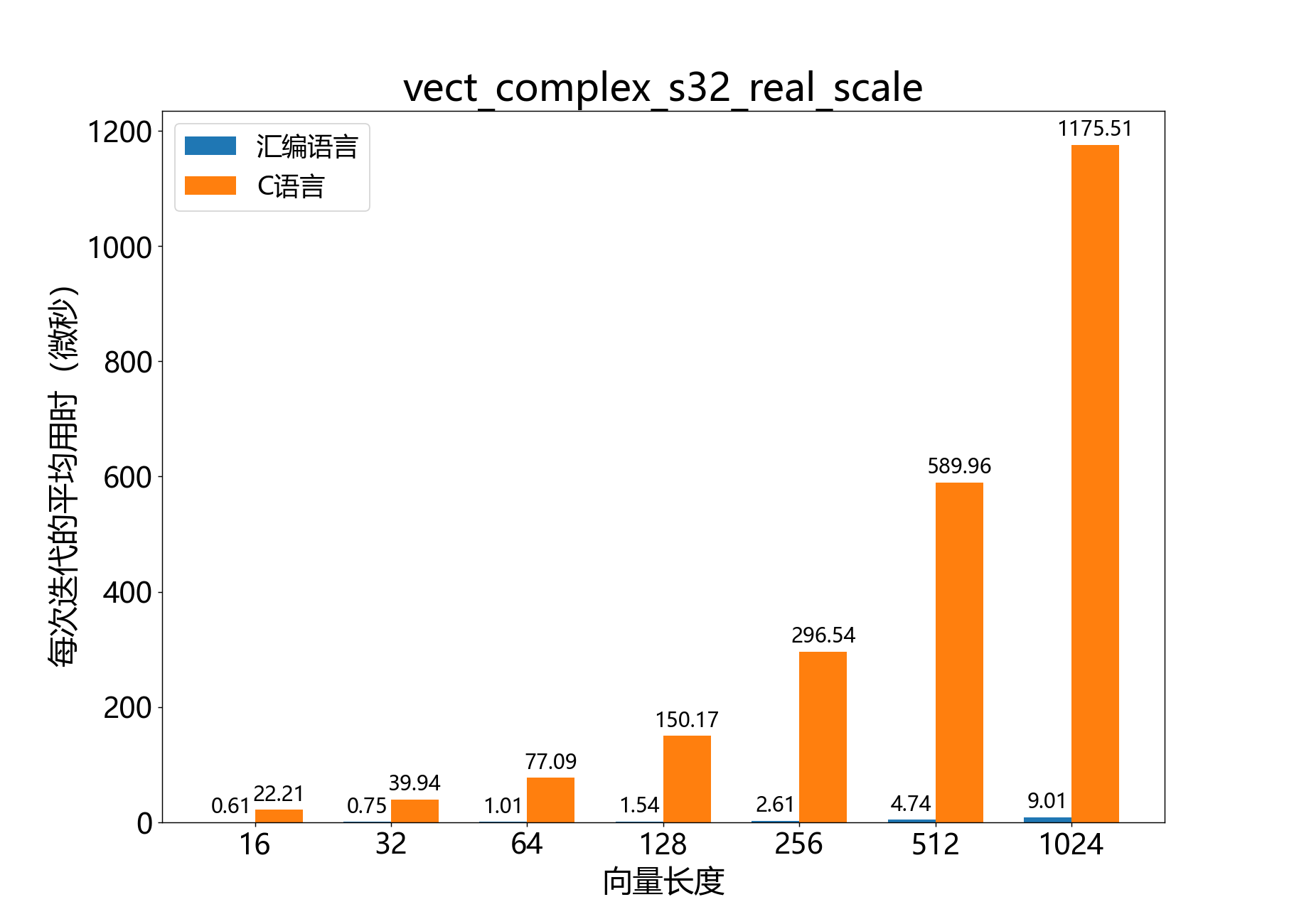
headroom_t vect_complex_s32_real_scale() 将复数32位向量乘以实数标量。
a[]和b[]分别表示复数32位尾数向量 a ˉ \bar{a} a ˉ b ˉ \bar{b} b ˉ c表示实数32位缩放因子 c c c
a[]和b[]必须从字对齐的地址开始。这个操作可以在b[]上安全地原地执行。
length是每个向量中的元素数量。
b_shr和c_shr是应用于 b ˉ \bar{b} b ˉ c c c
操作:
b k ′ ← s a t 32 ( ⌊ b k ⋅ 2 − b _ s h r ⌋ ) R e { a k } ← R e { b k ′ } ⋅ c I m { a k } ← I m { b k ′ } ⋅ c 其中 k ∈ 0 . . . ( l e n g t h − 1 ) \begin{split}\begin{align*} & b_k' \leftarrow sat_{32}(\lfloor b_k \cdot 2^{-b\_shr} \rfloor) \\ & Re\{a_k\} \leftarrow Re\{b_k'\} \cdot c \\ & Im\{a_k\} \leftarrow Im\{b_k'\} \cdot c \\ & \qquad\text{ 其中 }k\in 0\ ...\ (length-1) && \end{align*}\end{split} b k ′ ← s a t 32 (⌊ b k ⋅ 2 − b _ s h r ⌋) R e { a k } ← R e { b k ′ } ⋅ c I m { a k } ← I m { b k ′ } ⋅ c 其中 k ∈ 0 ... ( l e n g t h − 1 ) 块浮点数:
如果 b ˉ \bar{b} b ˉ b ˉ ⋅ 2 b _ e x p \bar{b} \cdot 2^{b\_exp} b ˉ ⋅ 2 b _ e x p c c c c ⋅ 2 c _ e x p c \cdot 2^{c\_exp} c ⋅ 2 c _ e x p a ˉ \bar{a} a ˉ a ˉ ⋅ 2 a _ e x p \bar{a} \cdot 2^{a\_exp} a ˉ ⋅ 2 a _ e x p a _ e x p = b _ e x p + c _ e x p + b _ s h r + c _ s h r a\_exp = b\_exp + c\_exp + b\_shr + c\_shr a _ e x p = b _ e x p + c _ e x p + b _ s h r + c _ s h r
函数vect_complex_s32_real_scale_prepare()可以根据输入指数 b _ e x p b\_exp b _ e x p c _ e x p c\_exp c _ e x p b _ h r b\_hr b _ h r c _ h r c\_hr c _ h r a _ e x p a\_exp a _ e x p b _ s h r b\_shr b _ s h r c _ s h r c\_shr c _ s h r
参数:
complex_s32_t a[] – [out]a ˉ \bar{a} a ˉ const complex_s32_t b[] – [in]b ˉ \bar{b} b ˉ const int32_t c – [in]c c c const unsigned length – [in]a ˉ \bar{a} a ˉ b ˉ \bar{b} b ˉ c ˉ \bar{c} c ˉ const right_shift_t b_shr – [in]b ˉ \bar{b} b ˉ const right_shift_t c_shr – [in]c c c
返回值:
异常:
如果a或b不是字对齐的,则引发ET_LOAD_STORE异常(参见笔记:向量对齐 )
参考性能 :
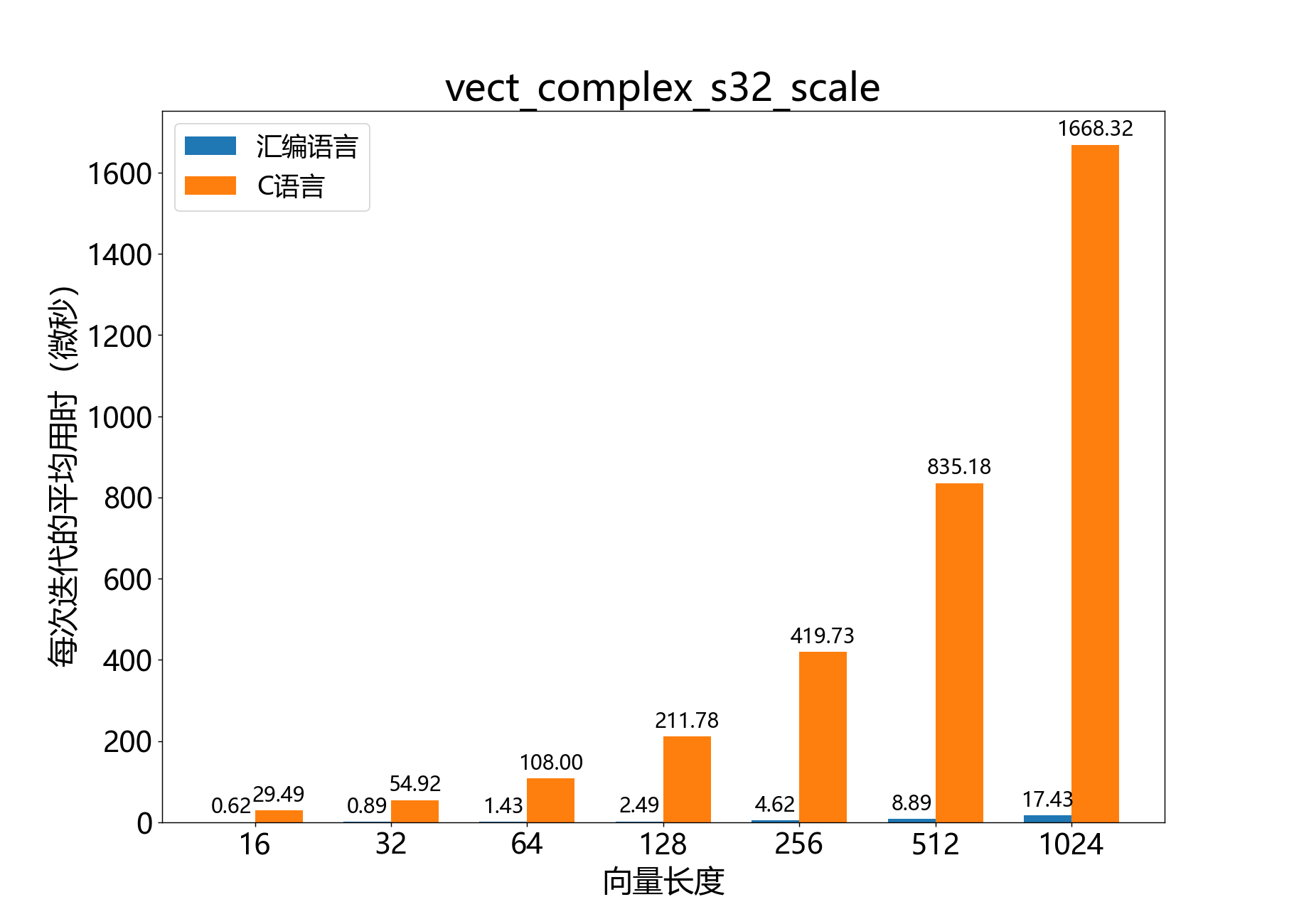
headroom_t vect_complex_s32_scale() 将复数32位向量乘以复数32位标量。
a[]和b[]分别表示复数32位尾数向量 a ˉ \bar{a} a ˉ b ˉ \bar{b} b ˉ
c表示复数32位缩放因子 c c c
a[]和b[]必须从字对齐的地址开始。该操作可以在b[]上安全地原地执行。
length是每个向量中的元素数量。
b_shr和c_shr是应用于每个 b ˉ \bar{b} b ˉ c c c
操作:
b k ′ ← s a t 32 ( ⌊ b k ⋅ 2 − b _ s h r ⌋ ) R e { a k } ← ( R e { v k } ⋅ R e { c } − I m { v k } ⋅ I m { c } ) ⋅ 2 − 30 I m { a k } ← ( R e { v k } ⋅ I m { c } + I m { v k } ⋅ R e { c } ) ⋅ 2 − 30 其中 k ∈ 0 . . . ( l e n g t h − 1 ) \begin{align*}
& b_k' \leftarrow sat_{32}(\lfloor b_k \cdot 2^{-b\_shr} \rfloor) \\
& Re\{a_k\} \leftarrow \left( Re\{v_k\} \cdot Re\{c\} - Im\{v_k\} \cdot Im\{c\} \right) \cdot 2^{-30} \\
& Im\{a_k\} \leftarrow \left( Re\{v_k\} \cdot Im\{c\} + Im\{v_k\} \cdot Re\{c\} \right) \cdot 2^{-30} \\
& \qquad\text{ 其中 }k\in 0\ ...\ (length-1) &&
\end{align*} b k ′ ← s a t 32 (⌊ b k ⋅ 2 − b _ s h r ⌋) R e { a k } ← ( R e { v k } ⋅ R e { c } − I m { v k } ⋅ I m { c } ) ⋅ 2 − 30 I m { a k } ← ( R e { v k } ⋅ I m { c } + I m { v k } ⋅ R e { c } ) ⋅ 2 − 30 其中 k ∈ 0 ... ( l e n g t h − 1 ) 如果 b ˉ \bar{b} b ˉ b ˉ ⋅ 2 b _ e x p \bar{b} \cdot 2^{b\_exp} b ˉ ⋅ 2 b _ e x p c c c c ⋅ 2 c _ e x p c \cdot 2^{c\_exp} c ⋅ 2 c _ e x p a ˉ \bar{a} a ˉ a ˉ ⋅ 2 a _ e x p \bar{a} \cdot 2^{a\_exp} a ˉ ⋅ 2 a _ e x p a _ e x p = b _ e x p + c _ e x p + b _ s h r + c _ s h r a\_exp = b\_exp + c\_exp + b\_shr + c\_shr a _ e x p = b _ e x p + c _ e x p + b _ s h r + c _ s h r
可以使用函数 vect_complex_s32_mul_prepare() 根据输入指数 b _ e x p b\_exp b _ e x p c _ e x p c\_exp c _ e x p b _ h r b\_hr b _ h r c _ h r c\_hr c _ h r a _ e x p a\_exp a _ e x p b _ s h r b\_shr b _ s h r c _ s h r c\_shr c _ s h r
参数:
complex_s32_t a[] – [out]a ˉ \bar{a} a ˉ const complex_s32_t b[] – [in]b ˉ \bar{b} b ˉ const int32_t c_real – [in]c c c const int32_t c_imag – [in]c c c const unsigned length – [in]a ˉ \bar{a} a ˉ b ˉ \bar{b} b ˉ const right_shift_t b_shr – [in]b ˉ \bar{b} b ˉ const right_shift_t c_shr – [in]c c c
返回值:
异常:
如果a或b不是字对齐的,则引发ET_LOAD_STORE异常(参见 笔记:向量对齐 )
参考性能 :
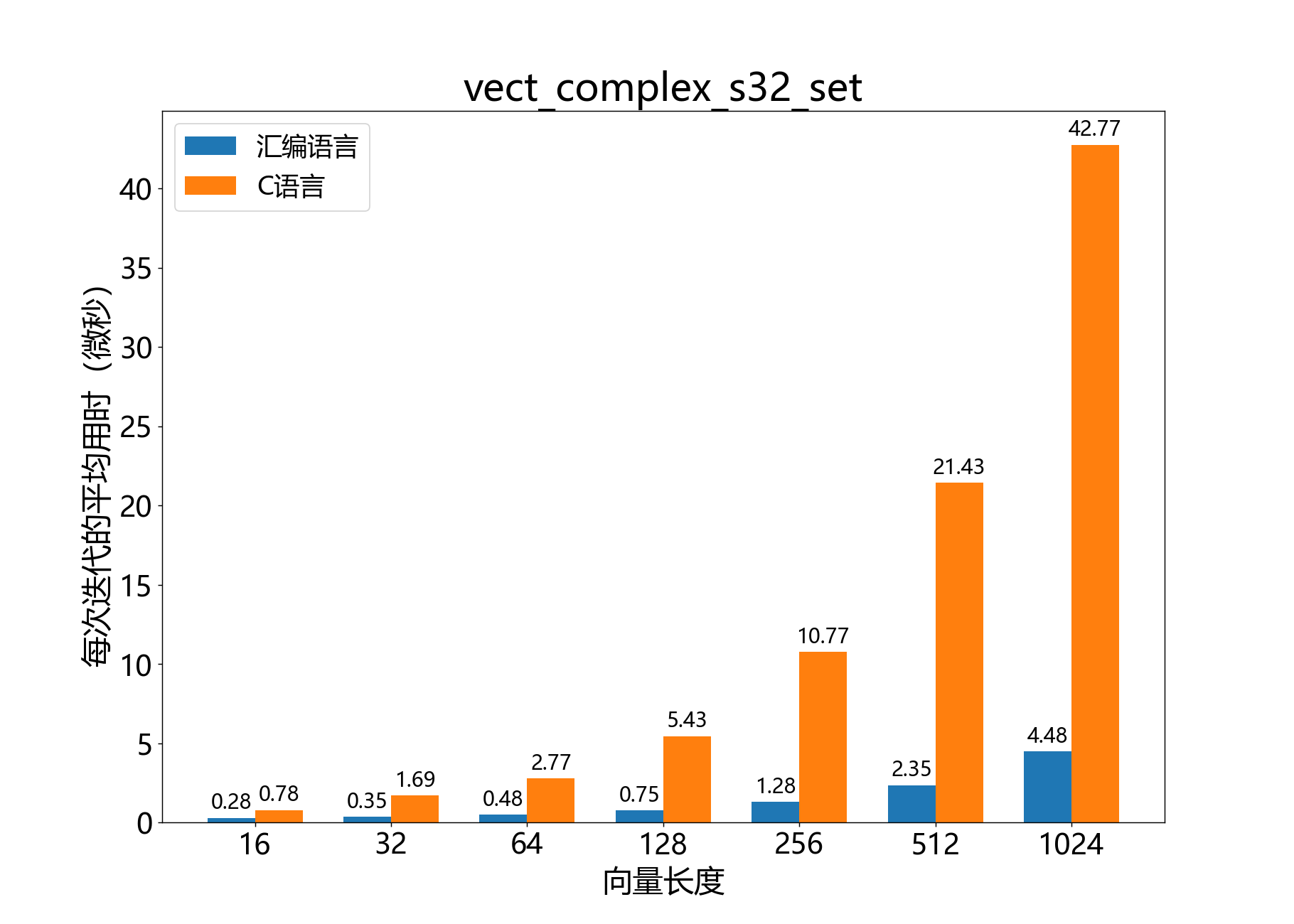
void vect_complex_s32_set() 将复数32位向量的每个元素设置为指定值。
a[]表示复数32位向量 a ˉ \bar{a} a ˉ a[]必须从字对齐的地址开始。
b_real和b_imag是要设置为每个元素的实部和虚部的值。
length是a[]中的元素数量。
操作:
a k ← b _ r e a l + j ⋅ b _ i m a g 其中 k ∈ 0 . . . ( l e n g t h − 1 ) 其中 j 2 = − 1 \begin{align*}
& a_k \leftarrow b\_real + j\cdot b\_imag \\
& \qquad\text{ 其中 }k\in 0\ ...\ (length-1) \\
& \qquad\text{ 其中 } j^2 = -1
\end{align*} a k ← b _ re a l + j ⋅ b _ ima g 其中 k ∈ 0 ... ( l e n g t h − 1 ) 其中 j 2 = − 1 如果 b b b b ⋅ 2 b _ e x p b \cdot 2^{b\_exp} b ⋅ 2 b _ e x p a ˉ \bar{a} a ˉ a ˉ ⋅ 2 a _ e x p \bar{a} \cdot 2^{a\_exp} a ˉ ⋅ 2 a _ e x p a _ e x p = b _ e x p a\_exp = b\_exp a _ e x p = b _ e x p
参数:
complex_s32_t a[] – [out]a ˉ \bar{a} a ˉ const int32_t b_real – [in]a ˉ \bar{a} a ˉ const int32_t b_imag – [in]a ˉ \bar{a} a ˉ const unsigned length – [in]a ˉ \bar{a} a ˉ
异常:
如果a不是字对齐的,则引发ET_LOAD_STORE异常(参见 笔记:向量对齐 )
参考性能 :
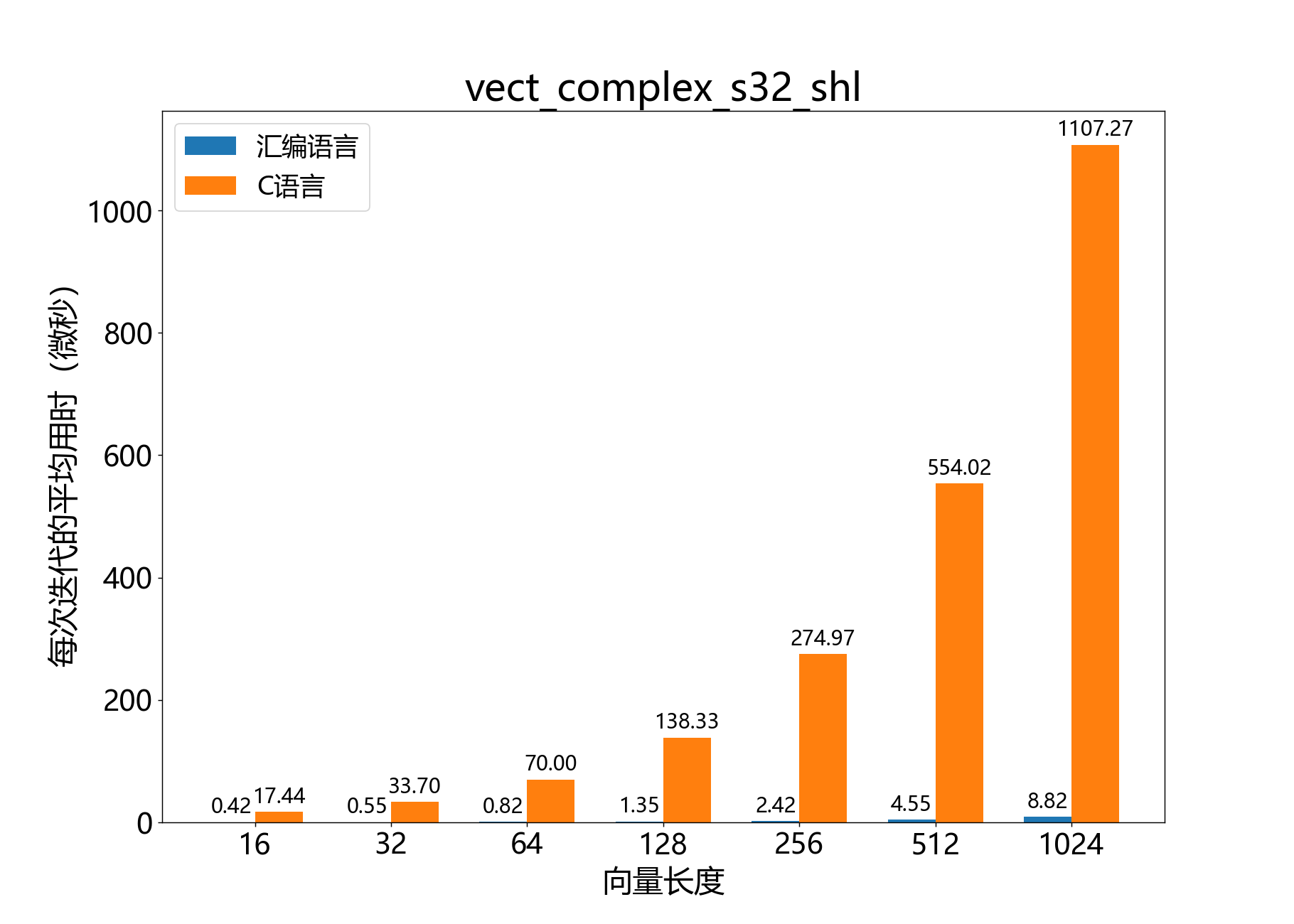
headroom_t vect_complex_s32_shl() 将复数32位向量的每个元素左移指定的位数。
a[]和b[]分别表示复数32位尾数向量 a ˉ \bar{a} a ˉ b ˉ \bar{b} b ˉ b[]上安全地原地执行。
length是向量 a ˉ \bar{a} a ˉ b ˉ \bar{b} b ˉ
b_shl是应用于 b ˉ \bar{b} b ˉ
操作:
R e { a k } ← s a t 32 ( ⌊ R e { b k } ⋅ 2 b _ s h l ⌋ ) I m { a k } ← s a t 32 ( ⌊ I m { b k } ⋅ 2 b _ s h l ⌋ ) 其中 k ∈ 0 . . . ( l e n g t h − 1 ) \begin{align*}
Re\{a_k\} & \leftarrow sat_{32}(\lfloor Re\{b_k\} \cdot 2^{b\_shl} \rfloor) \\
Im\{a_k\} & \leftarrow sat_{32}(\lfloor Im\{b_k\} \cdot 2^{b\_shl} \rfloor) \\
& \qquad\text{其中 }k\in 0\ ...\ (length-1)
\end{align*} R e { a k } I m { a k } ← s a t 32 (⌊ R e { b k } ⋅ 2 b _ s h l ⌋) ← s a t 32 (⌊ I m { b k } ⋅ 2 b _ s h l ⌋) 其中 k ∈ 0 ... ( l e n g t h − 1 ) 块浮点数:
如果 b ˉ \bar{b} b ˉ b ˉ ⋅ 2 b _ e x p \bar{b} \cdot 2^{b\_exp} b ˉ ⋅ 2 b _ e x p a ˉ \bar{a} a ˉ a ˉ ⋅ 2 a _ e x p \bar{a} \cdot 2^{a\_exp} a ˉ ⋅ 2 a _ e x p a ˉ = b ˉ ⋅ 2 b _ s h l \bar{a} = \bar{b} \cdot 2^{b\_shl} a ˉ = b ˉ ⋅ 2 b _ s h l a _ e x p = b _ e x p a\_exp = b\_exp a _ e x p = b _ e x p
参数:
complex_s32_t a[] – [out]a ˉ \bar{a} a ˉ const complex_s32_t b[] – [in]b ˉ \bar{b} b ˉ const unsigned length – [in]b ˉ \bar{b} b ˉ const left_shift_t b_shl – [in]b ˉ \bar{b} b ˉ
返回值:
异常:
如果a或b不是字对齐的,则引发ET_LOAD_STORE异常(参见 笔记:向量对齐 )
参考性能 :
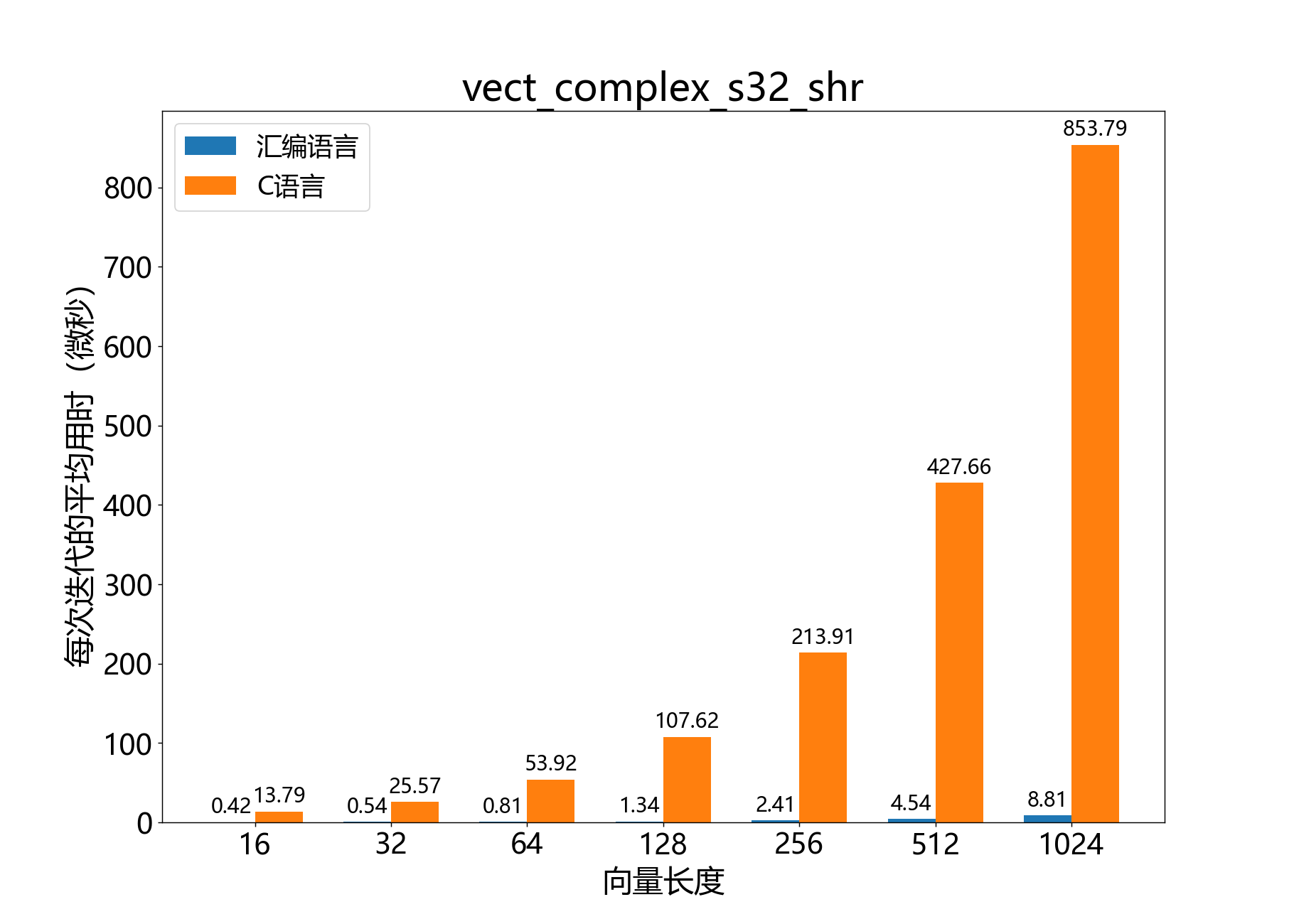
headroom_t vect_complex_s32_shr() 将复数32位向量的每个元素右移指定的位数。
a[]和b[]分别表示复数32位尾数向量 a ˉ \bar{a} a ˉ b ˉ \bar{b} b ˉ b[]上安全地原地执行。
length是向量 a ˉ \bar{a} a ˉ b ˉ \bar{b} b ˉ
b_shr是应用于 b ˉ \bar{b} b ˉ
操作:
R e { a k } ← s a t 32 ( ⌊ R e { b k } ⋅ 2 − b _ s h r ⌋ ) I m { a k } ← s a t 32 ( ⌊ I m { b k } ⋅ 2 − b _ s h r ⌋ ) 其中 k ∈ 0 . . . ( l e n g t h − 1 ) \begin{align*}
Re\{a_k\} & \leftarrow sat_{32}(\lfloor Re\{b_k\} \cdot 2^{-b\_shr} \rfloor) \\
Im\{a_k\} & \leftarrow sat_{32}(\lfloor Im\{b_k\} \cdot 2^{-b\_shr} \rfloor) \\
& \qquad\text{其中 }k\in 0\ ...\ (length-1)
\end{align*} R e { a k } I m { a k } ← s a t 32 (⌊ R e { b k } ⋅ 2 − b _ s h r ⌋) ← s a t 32 (⌊ I m { b k } ⋅ 2 − b _ s h r ⌋) 其中 k ∈ 0 ... ( l e n g t h − 1 ) 块浮点数:
如果 b ˉ \bar{b} b ˉ b ˉ ⋅ 2 b _ e x p \bar{b} \cdot 2^{b\_exp} b ˉ ⋅ 2 b _ e x p a ˉ \bar{a} a ˉ a ˉ ⋅ 2 a _ e x p \bar{a} \cdot 2^{a\_exp} a ˉ ⋅ 2 a _ e x p a ˉ = b ˉ ⋅ 2 − b _ s h r \bar{a} = \bar{b} \cdot 2^{-b\_shr} a ˉ = b ˉ ⋅ 2 − b _ s h r a _ e x p = b _ e x p a\_exp = b\_exp a _ e x p = b _ e x p
参数:
complex_s32_t a[] – [out]a ˉ \bar{a} a ˉ const complex_s32_t b[] – [in]b ˉ \bar{b} b ˉ const unsigned length – [in]b ˉ \bar{b} b ˉ const right_shift_t b_shr – [in]b ˉ \bar{b} b ˉ
返回值:
异常:
如果a或b不是字对齐的,则引发ET_LOAD_STORE异常(参见 笔记:向量对齐 )
参考性能 :
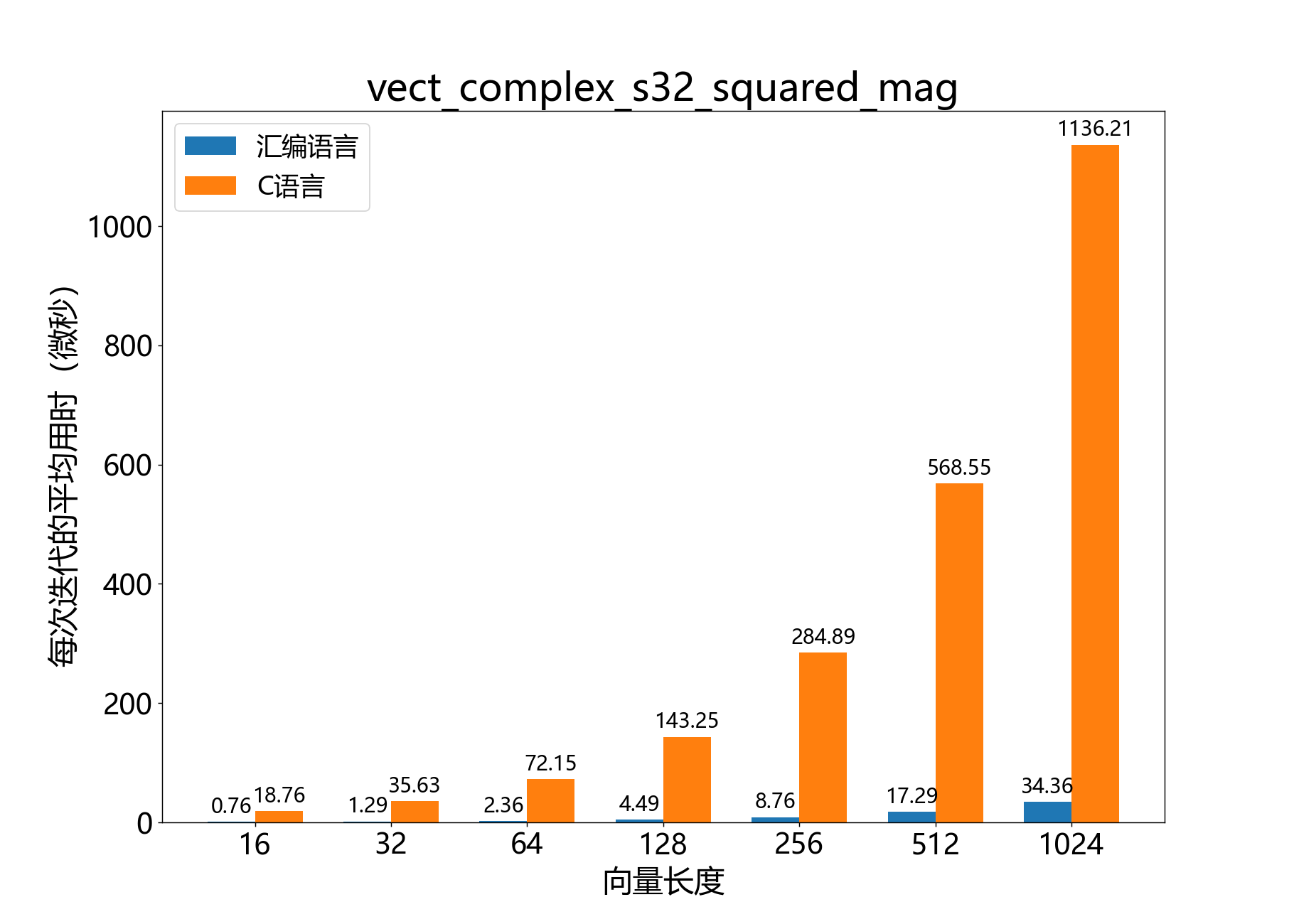
headroom_t vect_complex_s32_squared_mag() 计算复数32位向量元素的平方幅值。
a[]表示复数32位尾数向量 a ˉ \bar{a} a ˉ b[]表示实数32位尾数向量 b ˉ \bar{b} b ˉ
length是向量 a ˉ \bar{a} a ˉ b ˉ \bar{b} b ˉ
b_shr是应用于 b ˉ \bar{b} b ˉ
操作:
b k ′ ← s a t 32 ( ⌊ b k ⋅ 2 − b _ s h r ⌋ ) a k ← ( ( R e { b k ′ } ) 2 + ( I m { b k ′ } ) 2 ) ⋅ 2 − 30 其中 k ∈ 0 . . . ( l e n g t h − 1 ) \begin{align*}
b_k' & \leftarrow sat_{32}(\lfloor b_k \cdot 2^{-b\_shr} \rfloor) \\
a_k & \leftarrow ((Re\{b_k'\})^2 + (Im\{b_k'\})^2)\cdot 2^{-30} \\
& \qquad\text{其中 }k\in 0\ ...\ (length-1)
\end{align*} b k ′ a k ← s a t 32 (⌊ b k ⋅ 2 − b _ s h r ⌋) ← (( R e { b k ′ } ) 2 + ( I m { b k ′ } ) 2 ) ⋅ 2 − 30 其中 k ∈ 0 ... ( l e n g t h − 1 ) 块浮点数:
如果 b ˉ \bar{b} b ˉ b ˉ ⋅ 2 b _ e x p \bar{b} \cdot 2^{b\_exp} b ˉ ⋅ 2 b _ e x p a ˉ \bar{a} a ˉ a ˉ ⋅ 2 a _ e x p \bar{a} \cdot 2^{a\_exp} a ˉ ⋅ 2 a _ e x p a _ e x p = 2 ⋅ ( b _ e x p + b _ s h r ) a\_exp = 2 \cdot (b\_exp + b\_shr) a _ e x p = 2 ⋅ ( b _ e x p + b _ s h r )
函数 vect_complex_s32_squared_mag_prepare() 可以根据输入指数 b _ e x p b\_exp b _ e x p b _ h r b\_hr b _ h r a _ e x p a\_exp a _ e x p b _ s h r b\_shr b _ s h r
参数:
int32_t a[] – [out]a ˉ \bar{a} a ˉ const complex_s32_t b[] – [in]b ˉ \bar{b} b ˉ const unsigned length – [in]a ˉ \bar{a} a ˉ b ˉ \bar{b} b ˉ const right_shift_t b_shr – [in]b ˉ \bar{b} b ˉ
异常:
如果a不是双字对齐的或b不是字对齐的,则引发ET_LOAD_STORE异常(参见 笔记:向量对齐 )
返回值:
另请参阅:
vect_complex_s32_squared_mag_prepare
参考性能 :
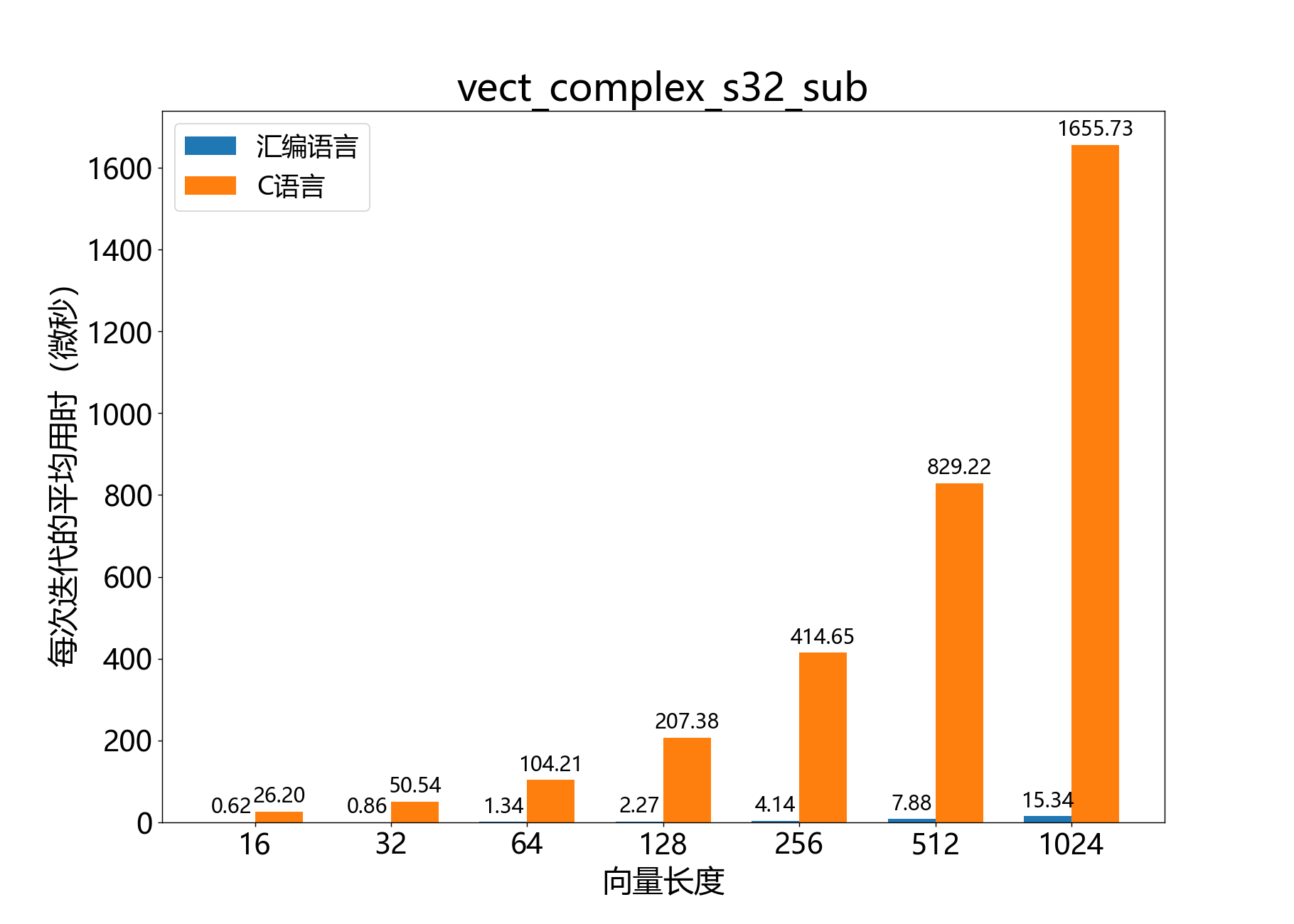
headroom_t vect_complex_s32_sub() 从一个复数32位向量中减去另一个复数32位向量。
参数a[]、b[]和c[]分别表示复数32位尾数向量 a ˉ \bar{a} a ˉ b ˉ \bar{b} b ˉ c ˉ \bar{c} c ˉ b[]或c[]上安全地原地执行。
length是向量中的元素数量。
b_shr和c_shr是应用于b ˉ \bar{b} b ˉ c ˉ \bar{c} c ˉ
操作:
b k ′ ← s a t 32 ( ⌊ b k ⋅ 2 − b _ s h r ⌋ ) c k ′ ← s a t 32 ( ⌊ c k ⋅ 2 − c _ s h r ⌋ ) R e { a k } ← R e { b k ′ } − R e { c k ′ } I m { a k } ← I m { b k ′ } − I m { c k ′ } 其中 k ∈ 0 . . . ( l e n g t h − 1 ) \begin{align*}
& b_k' \leftarrow sat_{32}(\lfloor b_k \cdot 2^{-b\_shr} \rfloor) \\
& c_k' \leftarrow sat_{32}(\lfloor c_k \cdot 2^{-c\_shr} \rfloor) \\
& Re\{a_k\} \leftarrow Re\{b_k'\} - Re\{c_k'\} \\
& Im\{a_k\} \leftarrow Im\{b_k'\} - Im\{c_k'\} \\
& \qquad\text{ 其中 }k\in 0\ ...\ (length-1)
\end{align*} b k ′ ← s a t 32 (⌊ b k ⋅ 2 − b _ s h r ⌋) c k ′ ← s a t 32 (⌊ c k ⋅ 2 − c _ s h r ⌋) R e { a k } ← R e { b k ′ } − R e { c k ′ } I m { a k } ← I m { b k ′ } − I m { c k ′ } 其中 k ∈ 0 ... ( l e n g t h − 1 ) 块浮点数:
如果b ˉ \bar{b} b ˉ c ˉ \bar{c} c ˉ b ˉ ⋅ 2 b _ e x p \bar{b} \cdot 2^{b\_exp} b ˉ ⋅ 2 b _ e x p c ˉ ⋅ 2 c _ e x p \bar{c} \cdot 2^{c\_exp} c ˉ ⋅ 2 c _ e x p a ˉ \bar{a} a ˉ a ˉ ⋅ 2 a _ e x p \bar{a} \cdot 2^{a\_exp} a ˉ ⋅ 2 a _ e x p
在这种情况下,必须选择b _ s h r b\_shr b _ s h r c _ s h r c\_shr c _ s h r a _ e x p = b _ e x p + b _ s h r = c _ e x p + c _ s h r a\_exp = b\_exp + b\_shr = c\_exp + c\_shr a _ e x p = b _ e x p + b _ s h r = c _ e x p + c _ s h r
函数vect_complex_s32_sub_prepare()可以根据输入指数b _ e x p b\_exp b _ e x p c _ e x p c\_exp c _ e x p b _ h r b\_hr b _ h r c _ h r c\_hr c _ h r a _ e x p a\_exp a _ e x p b _ s h r b\_shr b _ s h r c _ s h r c\_shr c _ s h r
参数:
complex_s32_t a[] – [out]a ˉ \bar{a} a ˉ
const complex_s32_t b[] – [in]b ˉ \bar{b} b ˉ
const complex_s32_t c[] – [in]c ˉ \bar{c} c ˉ
const unsigned length – [in]a ˉ \bar{a} a ˉ b ˉ \bar{b} b ˉ c ˉ \bar{c} c ˉ
const right_shift_t b_shr – [in]b ˉ \bar{b} b ˉ
const right_shift_t c_shr – [in]c ˉ \bar{c} c ˉ
返回值: 输出向量 a ˉ \bar{a} a ˉ
异常: ��如果a、b或c不是字对齐的,则引发ET_LOAD_STORE异常(参见 笔记:向量对齐 )
另请参阅: vect_complex_s32_sub_prepare
参考性能 :
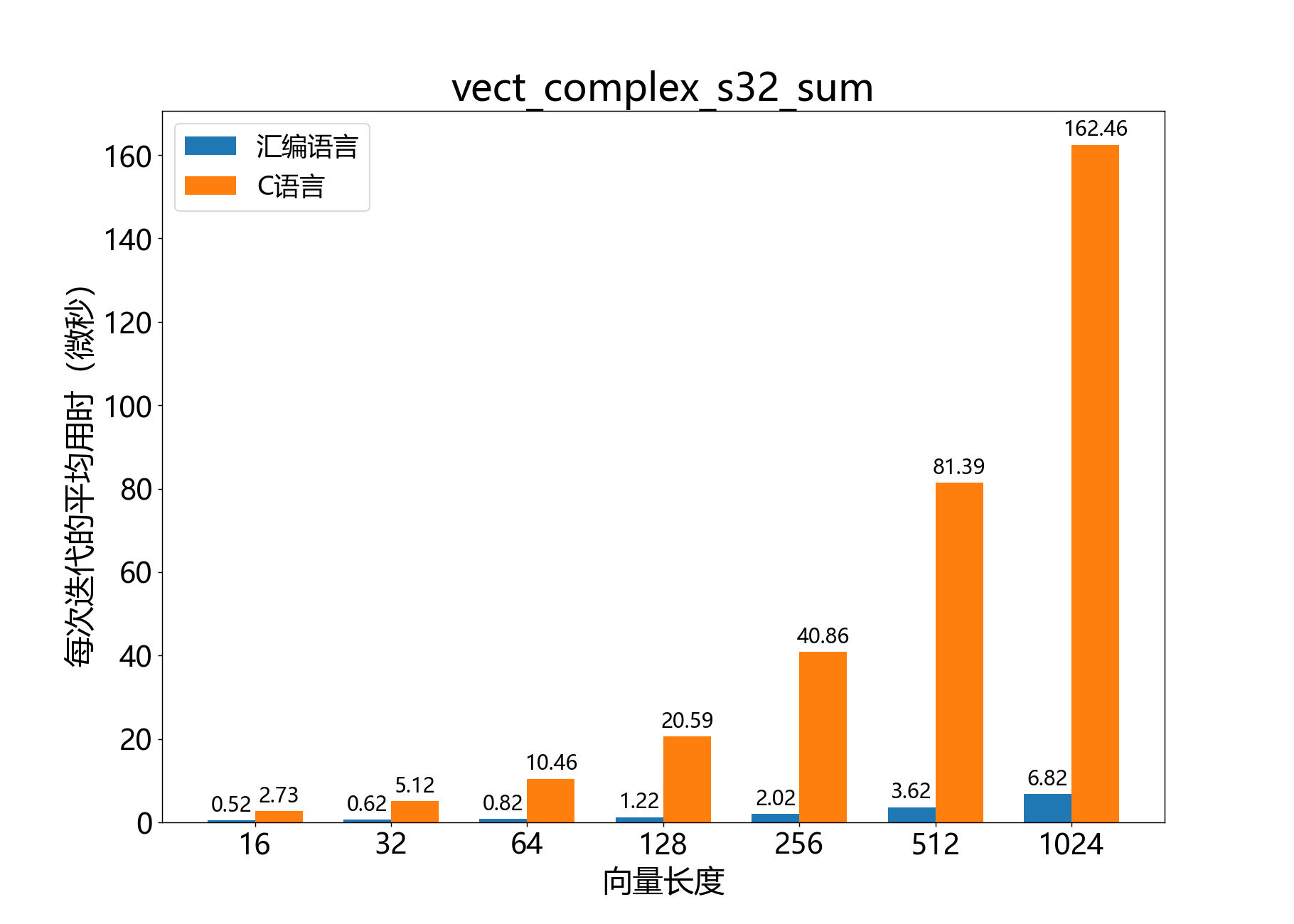
void vect_complex_s32_sum() 计算复数32位向量的元素和。
a是结果和的复数64位尾数。
b[]表示复数32位尾数向量 b ˉ \bar{b} b ˉ b[]必须从字对齐的地址开始。
length是向量 b ˉ \bar{b} b ˉ
b_shr是应用于b ˉ \bar{b} b ˉ 无符号 算术右移。
操作:
b k ′ ← b k ⋅ 2 − b _ s h r R e { a } ← ∑ k = 0 l e n g t h − 1 ( R e { b k ′ } ) I m { a } ← ∑ k = 0 l e n g t h − 1 ( I m { b k ′ } ) \begin{align*}
& b_k' \leftarrow b_k \cdot 2^{-b\_shr} \\
& Re\{a\} \leftarrow \sum_{k=0}^{length-1} \left( Re\{b_k'\} \right) \\
& Im\{a\} \leftarrow \sum_{k=0}^{length-1} \left( Im\{b_k'\} \right)
\end{align*} b k ′ ← b k ⋅ 2 − b _ s h r R e { a } ← k = 0 ∑ l e n g t h − 1 ( R e { b k ′ } ) I m { a } ← k = 0 ∑ l e n g t h − 1 ( I m { b k ′ } ) 块浮点数:
如果b ˉ \bar{b} b ˉ b ˉ ⋅ 2 b _ e x p \bar{b} \cdot 2^{b\_exp} b ˉ ⋅ 2 b _ e x p a a a a ⋅ 2 a _ e x p a \cdot 2^{a\_exp} a ⋅ 2 a _ e x p a _ e x p = b _ e x p + b _ s h r a\_exp = b\_exp + b\_shr a _ e x p = b _ e x p + b _ s h r
函数vect_complex_s32_sum_prepare()可以根据输入指数b _ e x p b\_exp b _ e x p c _ e x p c\_exp c _ e x p b _ h r b\_hr b _ h r c _ h r c\_hr c _ h r a _ e x p a\_exp a _ e x p b _ s h r b\_shr b _ s h r
额外细节:
内部上,和累积到四个不同的复数40位累加器中。这些累加器使用对称的40位饱和逻辑进行累加(范围为± 2 39 − 1 \pm 2^{39}-1 ± 2 39 − 1 a的64位字段中。在最后一步中,不应用饱和逻辑。
在最极端的情况下,每个b k b_k b k − 2 31 -2^{31} − 2 31 − 2 39 -2^{39} − 2 39 − 2 39 + 1 -2^{39}+1 − 2 39 + 1 4 ⋅ ( − 2 39 + 1 ) = − 2 41 + 4 4\cdot(-2^{39}+1) = -2^{41}+4 4 ⋅ ( − 2 39 + 1 ) = − 2 41 + 4
参数:
complex_s64_t* a – [out]a a a
const complex_s32_t b[] – [in]b ˉ \bar{b} b ˉ
const unsigned length – [in]b ˉ \bar{b} b ˉ
const right_shift_t b_shr – [in]b ˉ \bar{b} b ˉ
异常: 如果b不是字对齐的,则引发ET_LOAD_STORE异常(参见 笔记:向量对齐 )
另请参阅: vect_complex_s32_sum_prepare
参考性能 :
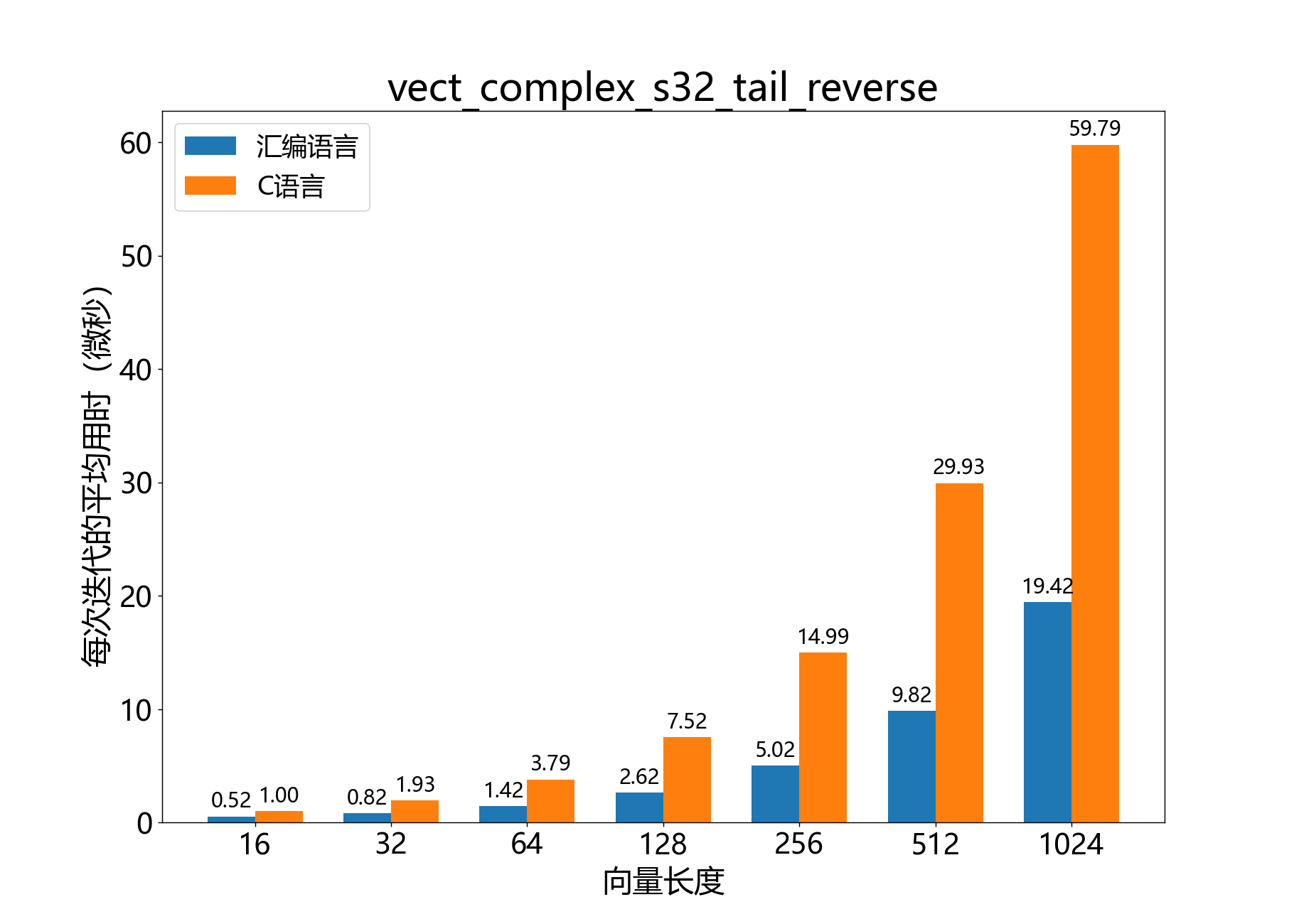
void vect_complex_s32_tail_reverse() 反转复数32位向量尾部的顺序。
该函数将复数32位向量 x ˉ \bar x x ˉ x ˉ \bar x x ˉ x 0 x_0 x 0 x 0 x_0 x 0 l e n g t h − 1 length-1 l e n g t h − 1
该函数在对一组实数值执行正向或反向FFT(即单声道FFT)时使用,并原地操作 x[]。
操作:
x 0 ← x 0 x k ← x l e n g t h − k 其中 k ∈ 1 … ( l e n g t h − 1 ) \begin{align*}
x_0 &\leftarrow x_0 \\
x_k &\leftarrow x_{length - k} \quad \text{其中 } k \in 1 \ldots (length-1)
\end{align*} x 0 x k ← x 0 ← x l e n g t h − k 其中 k ∈ 1 … ( l e n g t h − 1 ) 参数:
complex_s32_t x[] – [inout]const unsigned length – [in]x ˉ \bar x x ˉ
异常:
如果 x 不是字对齐的,则引发 ET_LOAD_STORE 异常(参见 笔记:向量对齐 )
参考性能 :
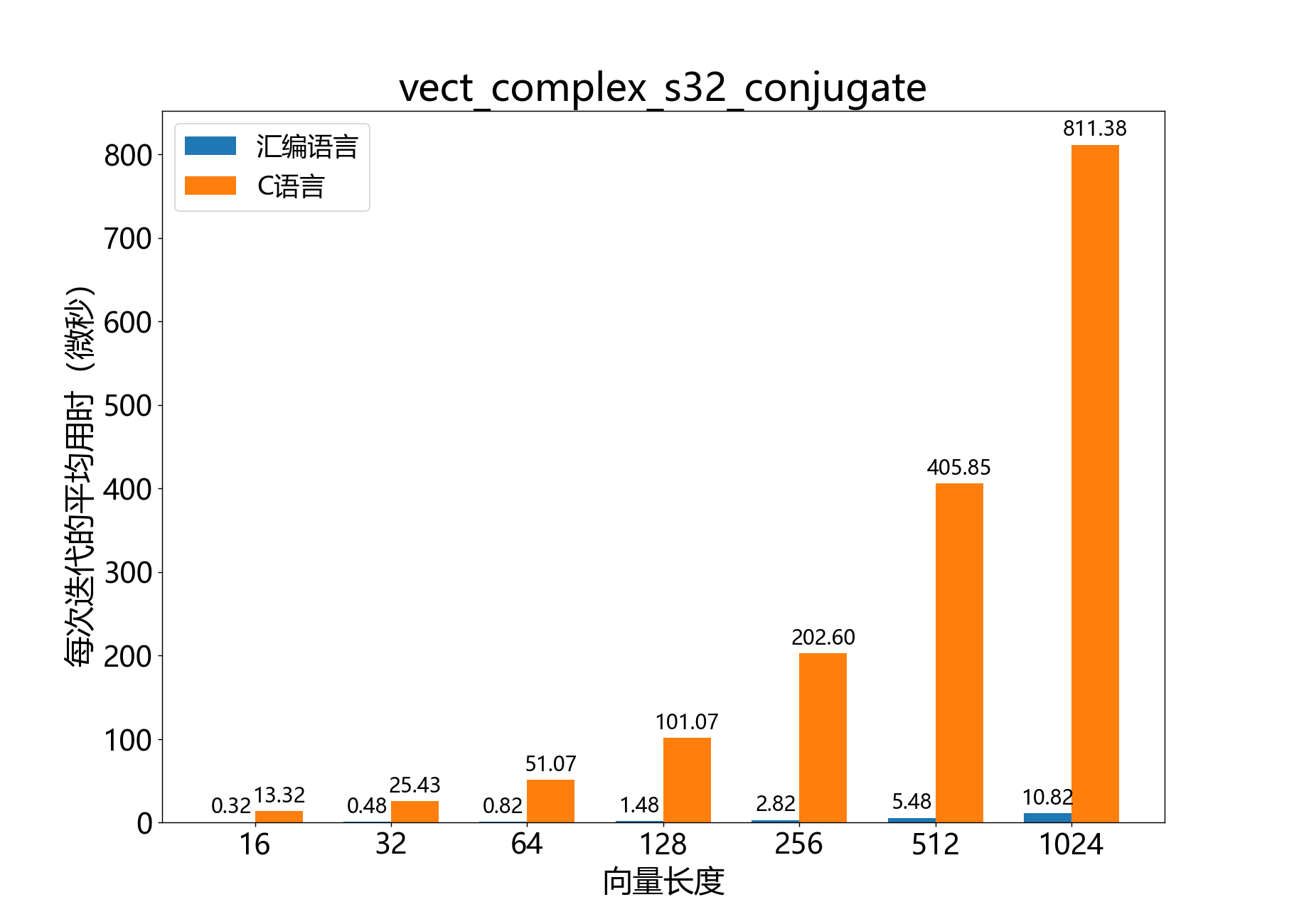
headroom_t vect_complex_s32_conjugate() 获取复数32位向量的共轭。
复数标量 z = x + y i z = x + yi z = x + y i z ∗ = x − y i z^* = x - yi z ∗ = x − y i b ˉ \bar b b ˉ a ˉ \bar a a ˉ
操作:
R e { a k } ← R e { b k } I m { a k } ← − I m { b k } 其中 k ∈ 1 . . . ( l e n g t h − 1 ) \begin{align*}
Re\{a_k\} &\leftarrow Re\{b_k\} \\
Im\{a_k\} &\leftarrow - Im\{b_k\} \\
&\qquad\text{其中 } k \in 1\ ...\ (length-1)
\end{align*} R e { a k } I m { a k } ← R e { b k } ← − I m { b k } 其中 k ∈ 1 ... ( l e n g t h − 1 ) 参数:
complex_s32_t a[] – [out]a ˉ \bar a a ˉ const complex_s32_t b[] – [in]b ˉ \bar b b ˉ const unsigned length – [in]a ˉ \bar a a ˉ b ˉ \bar b b ˉ
返回值:
异常:
如果 a 或 b 不是字对齐的,则引发 ET_LOAD_STORE 异常(参见 笔记:向量对齐 )
参考性能 :
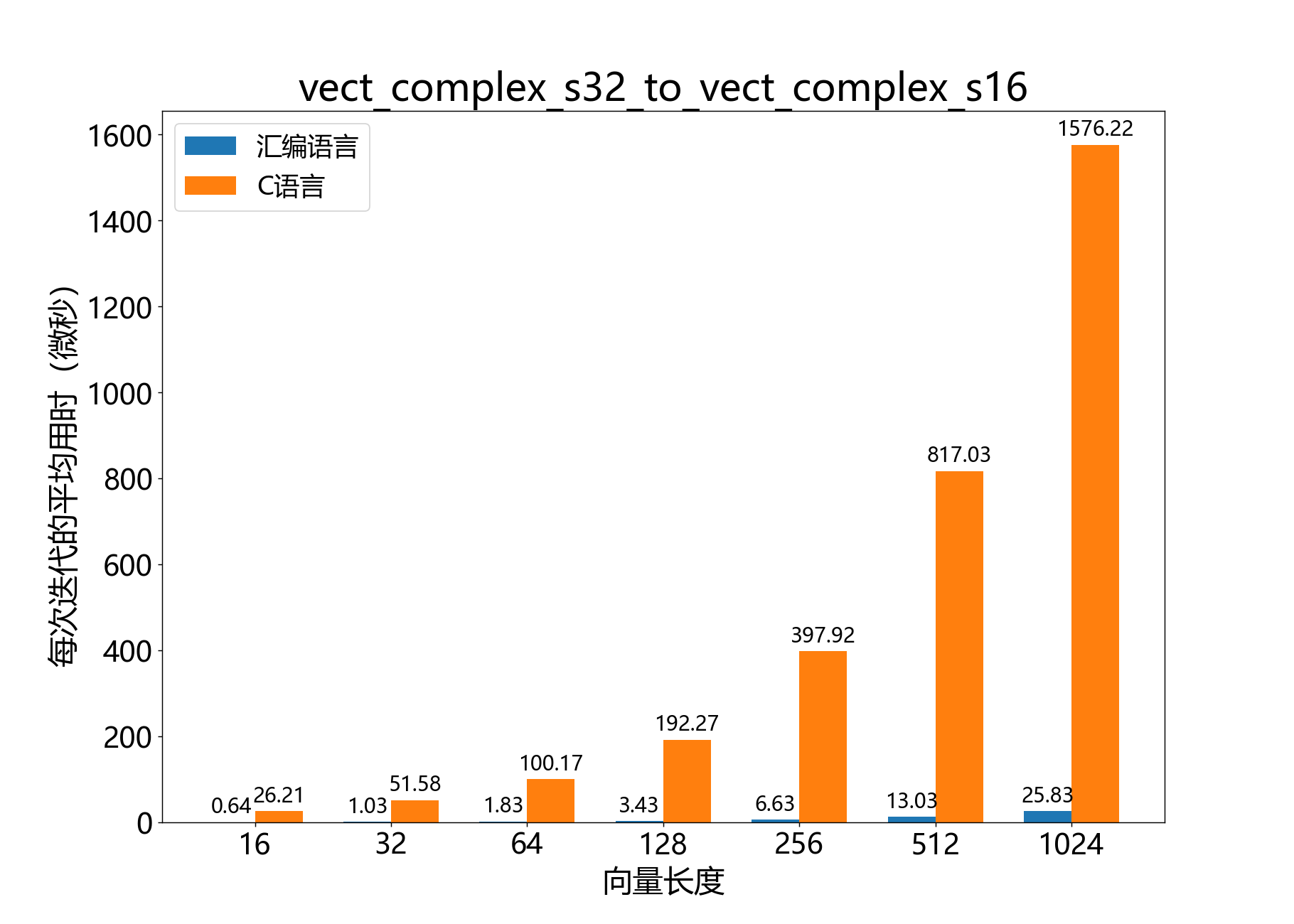
void vect_complex_s32_to_vect_complex_s16() 将复数32位向量转换为复数16位向量。
该函数将复数32位尾数向量 b ˉ \bar b b ˉ a ˉ \bar a a ˉ a ˉ ⋅ 2 a _ e x p \bar a \cdot 2^{a\_exp} a ˉ ⋅ 2 a _ e x p b ˉ ⋅ 2 b _ e x p \bar b \cdot 2^{b\_exp} b ˉ ⋅ 2 b _ e x p
在大多数情况下,b _ s h r b\_shr b _ s h r 16 − b _ h r 16 - b\_hr 16 − b _ h r b _ h r b\_hr b _ h r b ˉ \bar b b ˉ a _ e x p a\_exp a _ e x p a _ e x p = b _ e x p + b _ s h r a\_exp = b\_exp + b\_shr a _ e x p = b _ e x p + b _ s h r
操作:
b k ′ ← s a t 16 ( ⌊ b k ⋅ 2 − b _ s h r ⌋ ) R e { a k } ← R e { b k ′ } I m { a k } ← I m { b k ′ } 其中 k ∈ 0 . . . ( l e n g t h − 1 ) \begin{align*}
b_k' &\leftarrow sat_{16}(\lfloor b_k \cdot 2^{-b\_shr} \rfloor) \\
Re\{a_k\} &\leftarrow Re\{b_k'\} \\
Im\{a_k\} &\leftarrow Im\{b_k'\} \\
&\qquad\text{其中 } k \in 0\ ...\ (length-1)
\end{align*} b k ′ R e { a k } I m { a k } ← s a t 16 (⌊ b k ⋅ 2 − b _ s h r ⌋) ← R e { b k ′ } ← I m { b k ′ } 其中 k ∈ 0 ... ( l e n g t h − 1 ) 参数:
int16_t a_real[] – [out]a ˉ \bar a a ˉ int16_t a_imag[] – [out]a ˉ \bar a a ˉ const complex_s32_t b[] – [in]b ˉ \bar b b ˉ const unsigned length – [in]a ˉ \bar a a ˉ b ˉ \bar b b ˉ const right_shift_t b_shr – [in]b ˉ \bar b b ˉ
异常:
如果 a_real、a_imag 或 b 不是字对齐的,则引发 ET_LOAD_STORE 异常(参见 笔记:向量对齐 )
参考性能 :